Articles
Science et sociétés
Fonctions trigonométriques

Voici les 3 équations trigonométriques de base:

• Si cos x = b = cos a, alors
x = Arccos(b) = cos^-1(b) = a + 2kπ ou
x = - a + 2kπ , k ∈ Z

• Si sin x = b = sin a , alors
x = Arcsin(b) = sin^-1(b) = a + 2kπ ou
x = π - a + 2kπ , k ∈ Z

• Si tan x = b = tan a , alors
x = Arctan(b) = tan^-1(b) = a + kπ , k ∈ Z

Équations trigonométriques


Nous utliserons les formules suivantes:

cos(a + b) = cos a cos b - sin a sin b
cos(a - b) = cos a cos b + sin a sin b
Qui donnent:
2 cos a cos b = cos(a + b) + cos(a - b)
2 sin a sin b = cos(a - b) - cos(a + b

cos²a + sin² a = 1
sin (2a) = 2 sin a cos a
tan(a + b) = (tan a + tan b)/(1 - tan a tan b)
Qui donne :
tan(2a) = 2tan a/(1 - tan² a)

sin x + cos x = √ 2 sin (x + π/4)

cos (x) : fonction paire ⇒ cos(-x) = cos(x)
sin(x) : fonction impaire ⇒ sin(-x) = - sin(x)
tan x = sin x / cos x , avec cos x ≠ 0




Exercice

Soit h une fonction définie par :

h : x ---> h(x) = (1 - cos 2x)/sin 2x

1) a) Résolvons l'équation sin 2x = 0

sin 2x = 0 = sin 0 ⇒ 2x = 0 + 2kπ ou 2x = π - 0 + 2kπ ,

C'est à dire x = kπ ou x = π/2 + kπ , k ∈ Z

x = kπ ou x = π/2 + kπ , k ∈ Z

Le dénomonateur de la fraction définissant h(x) doit être non nul. C'est à dire sin(2x) ≠ 0, ou
x ≠ kπ et x ≠ π/2 + kπ , k ∈ Z

Ainsi, le domaine de définition D_h est :

D_h = R \ {kπ , π/2 + kπ , k ∈ Z }

ou

D_h = {∀ x ∈ R / x ≠ kπ et x ≠ π/2 + kπ , k ∈ Z }

b) • h(π/4) = (1 - cos (2π/4))/ sin (2π/4) =
= (1 - cos (π/2))/ sin (π/2) = (1 - 0)/ 1 = 1

h(π/4) = 1

• h(π/6) = (1 - cos (2π/6))/ sin (2π/6) =

= (1 - cos (π/3))/ sin (π/3) = (1 - 1/2)/ √3/2 = (1/2)/(√3/2) = √3/3

h(π/6) = √3/3

c) • h(- x) = (1 - cos (- 2x))/sin 2(- x) =
(1 - cos (2x))/- sin 2(x) = - (1 - cos (2x))/sin 2(x) = - h(x)

Conclusion:

h(- x) = - h(x) ⇒ la fonction h est impaire.

Démontrons la relation suivante:

h(π - x) = (1 - cos 2(π - x ))/sin 2(π - x)

On a:

Au numérateur:

cos 2(π - x ) = cos(2π - 2x) = cos (2π ) cos (-2x) - sin (2π) sin(-2x) = 1 cos 2x - 0 sin(-2x) = cos 2x

Numé(x) = 1 - cos 2(π - x ) = 1 - cos 2x

Numé(x) = 1 - cos 2(π - x ) = 1 - cos 2x

• Au dénominateur:

sin 2(π - x) = sin(2π - 2x) = sin(2π) cos (-2x) + cos (2π) sin (-2x) =
0 cos (-2x) + 1 sin (-2x) = - sin 2x

Déno(x) = - sin 2x

Déno(x) = - sin 2x

Il vient donc: h(π - x) = Numé(x) / Déno(x) =
1 - cos 2x / - sin2x = - (1 - cos 2x)/ sin 2x = - h(x)

Donc:

h(π - x) = - h(x)


2) a) h(x) = (1 - cos 2x)/sin 2x

On a :

cos 2x = cos (x + x) = cos x cosx - sin x sin x =
cos²x - sin² x

Donc :

Num(x) = 1 - cos 2x = 1 - cos²x + sin² x = 2 sin²x

D'autre part:

sin 2x = 2 sin x cos x . Il vient donc:

Dén(x) = 2 sin x cos x

Donc :

h(x) = Num(x)/Dén(x) = 2 sin²x / 2 sin x cos x

On réduit cette fraction en éliminant sin x, à condition qu'il soit ≠ 0. C'est à dire sin x ≠ 0 . D'où

x ≠ 0 + 2kπ = 2kπ et x ≠ π - 0 + 2kπ = π + 2kπ.

x ≠ 2kπ et x ≠ π + 2kπ k ∈ Z.       (R1)

Il reste donc:

h(x) = sin x / cos x = tan x

Mais cos x doit être aussi non nul, c'est à dire : cos x ≠ 0. D'où

x ≠ π/2 + 2kπ et x ≠ - π/2 + 2kπ k ∈ Z       (R2)

Dans le domaine de définition de la fonction h(x) , avec les restrictions (R1) et (R2), on peut ecrire:

∀ x ∈ ]0; +π/2[, h(x) = tan(x)

b) On va résoudre les équations:

a) h(x) = tan x = sin x /cos x

h(x) > 1 ⇒ sin x /cos x > 1

Dans ]0; +π/2[ cos x > 0 , l'inéquation devient:

sin x > cos x

sin x - cos x > 0

or

sin x - cos x = sin(x - π/4)/√2 /2

L'inéquation devient:

sin(x - π/4)/√2 /2 > 0
sin(x - π/4) > 0

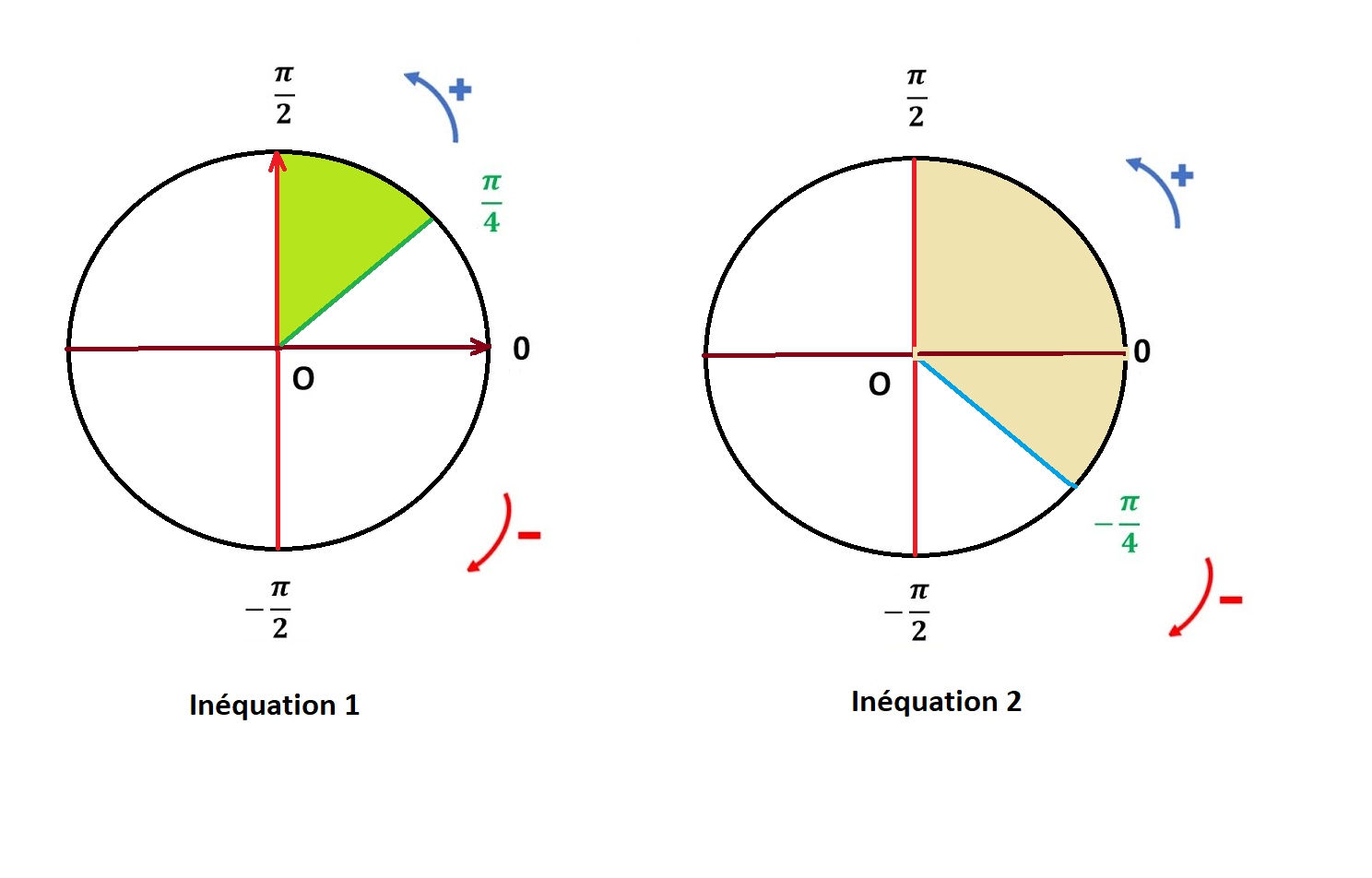
Dans ]0; +π/2[, la fonction sinus est croissante, donc:

sin(x - π/4) > sin 0 ⇒

x - π/4 > 0 + 2kπ, k ∈ Z, ou
x - π/4 π - 0 + 2kπ, k ∈ Z

x > π/4 + 2kπ, k ∈ Z, ou
x > π/4 + π + 2kπ, k ∈ Z

Ainsi, l'ensemble des solutions de l'inéquation, dans l'intervalle ]0, π/2[, avec h(x) = tan x est :

S = ]π/4, π/2[

b) Équation (2)

h(x) > 1 ⇒ sin x /cos x > - 1

ou

sin x + cos x > 0

or

sin x + cos x = sin(x + π/4)/√2 /2

L'inéquation devient:

sin(x + π/4)/√2 /2 > 0

sin(x + π/4) > 0

Dans ]0; +π/2[, la fonction sinus est croissante, donc:

sin(x + π/4) > sin 0 ⇒

x + π/4 > 0 + 2kπ, k ∈ Z, ou
x + π/4 π - 0 + 2kπ, k ∈ Z

x > - π/4 + 2kπ, k ∈ Z, ou
x > - π/4 + π + 2kπ, k ∈ Z

Ainsi, l'ensemble des solutions de l'inéquation, dans l'intervalle ]0, π/2[, avec h(x) = tan x est :

S = ]- π/4, π/2[

Avec h(x) qui prends son expression initiale , x est exclu, on aura:

S = ]- π/4, 0[ ∪ ]0, π/2[

-- Abdurrazzak Ajaja
novembre 2023