Mathématiques
Physique
Chimie
Calculateurs Scientifiques
© The scientific sentence. 2010

| |
|
Articles
Mathématiques
Barycentre , parallélogramme et vecteurs
Barycentre
Parallélogramme
Vecteurs
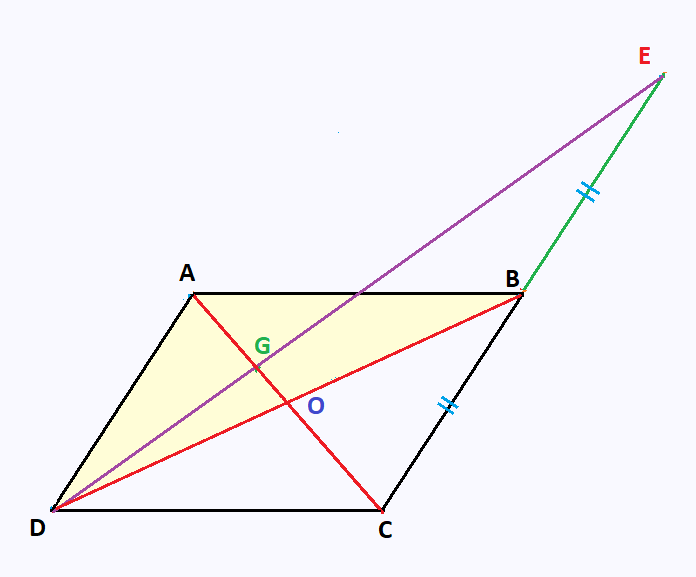
1. ABCD est un parallélogramme de centre O. G est le barycentre
des trois points pondérés (B,2), (C,-1) et (D,2). E est le barycentre des
deux points pondérés (B,2) et (C,-1).
On aura donc, O est considéré comme une origine:
OG = (2 OB + (-1)OC
+ 2 OD)/(2 + 2 - 1)
= (2 OB - OC
+ 2 OD)/3
Nous avons, puisque O est milieu de la diagonale du parallélogramme:
OB +
OD =
0
Donc:
OG
= - OC/3
OG = - OC/3 (1)
Nous avons aussi :
OE = 2 OB + (-1)OC
/(2 - 1)
= 2 OB - OC
OE = 2 OB - OC
(2)
1. Vérifions que B est milieu de [C,E]
Partons de
BC + BE =
0 (3)
=
BC +
BC +
CE
=
2BC +
CO +
OE
=
2BC +
CO +
2OB - OC
=
2CO +
2OC = 0
B est milieu de [C,E]
2.
AG = AB
+ BC + CG
= AB
+ AD + CO
+ OG
= AB
+ AD + CO
- (4/3)OC
= AB
+ AD + CO
- (2/3)AC
Nous avons dans le parallélogramme ABCD:
AB + AD =
+ AC
Donc :
AG = AC
- (2/3)AC =
(1/3)AC
AG =
(1/3)AC (4)
4. Le graphe est représenté ci-dessous .
5.
Rappel:
Le centre de gravité G d'un triangle est le point de concours des médianes
du triangle. Il se situe au tiers des médianes issues de leur « pied ».
Ici le pied considéré est le point A, et la médiane est le segment [AO]
dans le triangle ABD.
G est le centre de gravié du triangle ABD puisque, selon
la relation (4):
AG =
(1/3)AC
6. Montrons que les pointa D, G, et E sont alignés.
AG =
(1/3)AC
Nous avons:
DE =
DG + GE
On a :
GE = GC +
CE =
GA + AC +
+ CE
=
- (1/3) AC + AC +
+ 2 CB
= 2 DG
Donc:
DE = DG +
2 DG = 3 DG =
DE = 3 DG
⇔ Les points D, G, et E sont alignés.
7. L'ensemble des points tels que :
|| 2 MD - MC + 2 MB || =
3|| 2 MB - MC ||
Nous avons
|| 2 (MO + OD ) -
MO - OC+ 2 (MO +
OB) || =
|| 3 (MO + 2 OD )
- OC+ 2 (OB ||
=
|| 3(MO
- OC ||
=
|| 3 MO
+ 3 OG ||
=
|| 3(MG ||
Ainsi:
|| 2 MD - MC + 2 MB || =
|| 3(MG ||
Pour le second membre:
3|| 2 MB - MC ||
=
3|| 2 MC + 2 CB
- MC ||
=
3|| MC + 2 CB
||
=
3|| MO +OC +
2 CO + 2 OB
||
=
3|| MO - OC +
2 OB
||
=
3|| MO + OE
||
=
3|| ME
||
Ainsi:
|| 2 MD - MC + 2 MB || =
3|| ME
||
L'égalité devient:
|| 3(MG || = 3|| ME ||
C'est à dire :
|| (MG || = || ME ||
L'ensemble des points M est la médiatrice du segment [G,E].
8. L'ensemble des points tels que :
1 ≤ || 2 MB - MC || ≤ 2
Nous avonsd déjà trouvé
|| 2 MB - MC || =
|| ME ||
Alors:
1 ≤ || ME || ≤ 2
L'ensemble des points M est un cercle de centre E et de rayon
compris dans l'intervalle [1,2].
9. L'ensemble des points tels que :
|| 2 MD - MC + 2 MB || =
|| 2 MA - MB - MC ||
Nous avons montré que:
|| 2 MD - MC + 2 MB || =
|| 3(MG ||
Maintenant:
|| 2 MA - MB - MC || =
|| 2 MO + 2 OA
- MO - OB - MO
- OC ||
|| OA
- OB+ OA - OC
||
|| BA
+ CA
||
|| AB
+ AC
||
Donc:
|| MG ||=
(1/3)||AB
+ AC||
L'ensemble des points M est un cercle de rayon || AB
+ AC
||/3.
-- Abdurrazzak Ajaja
novembre 2023
|
|