Mathématiques
Physique
Chimie
Calculateurs Scientifiques
© The scientific sentence. 2010

| |
|
Articles
Science and societies
Mécanique
Mécanique
Mouvement de rotation
Travail et puissance d'une force
Seule travaille la composante tangentielle mgsinθ du poid
P = mg, d'un corps sur un plan incliné d'un angle θ par raport à
l'horizontale.

1. Travail du poids de m sur à la
fin du segment rectiligne AB:
W(
P
) = + m g H , H = AB sin θ
W(
P
) = m g AB sin θ = 0.5 x 10 x 2 x sin 60 = 5 √3 = + 8.66 Joules
W(
P
) = + 8.66 Joules
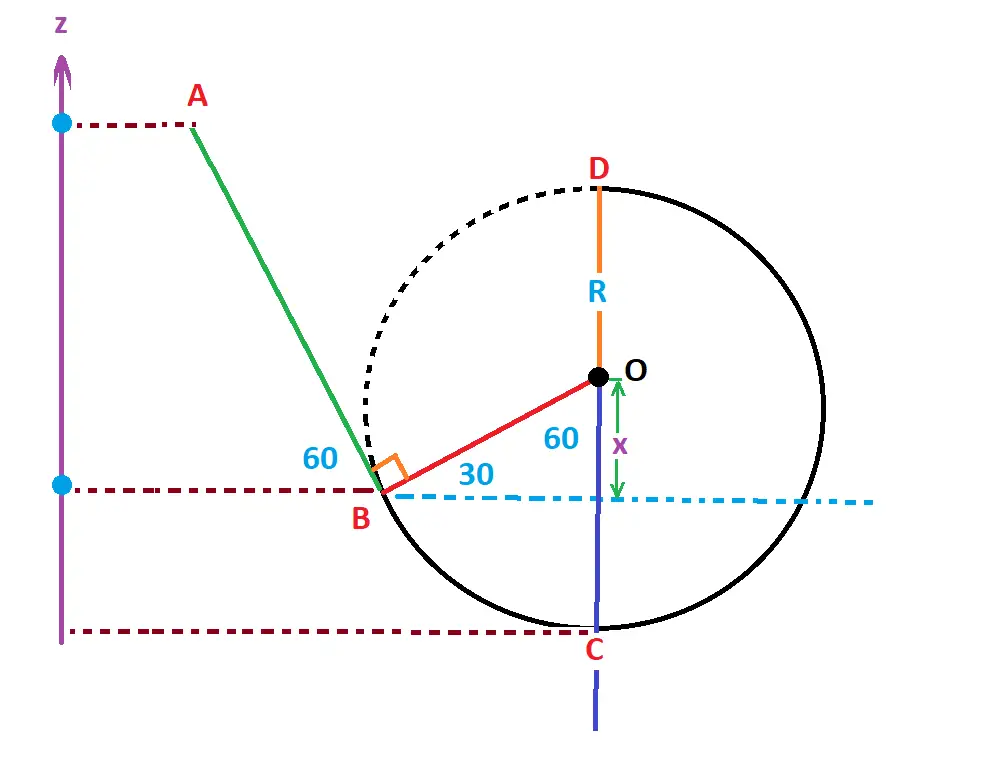
2. Travail du poids de m sur l'arc BC:
Nous avons x = R sin 30 = R/2
W(
P
)(B,C) = + m g R/2 = 0.5 x 10 x 0.5/2
= 5/4 = + 1.25 Joules
3. Travail du poids de m sur l'arc CD:
W(
P
)(C,D) = - m g x 2R = - 0.5 x 10 x 2 x 0.5 = - 5 Joules
3. Travail du poids de m sur l'arc BD:
W(
P
)(B,D) = W(
P
) (B,C) + W(
P
)(C,D) =
mgR/2 - 2mgR = (1/2 - 2) mgR = -(3/2) mgr =
1.25 - 5 = - 3.75 Joules.
W(
P
)(B,D) = - 3.75 Joules.
2.
a)
Rappelons que lorsqu'il n'y a pas de frottement sur un
plan, alors la réaction du plan sur l'objet glissant se
réduit à la normale :
N
=
R
Le travail de la réaction R sur tout le trajet AD
est réduit au travail des frottements, puisque la
composante normale N ne travail pas: W(N) = 0.
Le long du trajet:
W (
R
) = w(
f
)AD =
W(
f
) AB + W(f) BC + W(
f
) CD =
- f x AB - f arc(BC) - f x arc(CD)
Nous avons : arc(BC) + arc(CD) = arc (BD)=
R x (60 + 180) degrés = R x 240 x π/180 radians.
Donc:
W AD(
R
) = W AD(
f
) =
- f x AB - f x R x 240 x π/180
= - f (AB + R x 240 x π/180)= - f ( 2 + R x 4π/3)
= - 2 f(1 + 2Rπ/3)
= - 2 x 0.9 ( 1 + π/3) =
= - 3.68 Joules.
W AD(
R
) = - 3.68 Joules.
La valeure est négative., le travail est résistant.
b) L'intensité de la force de frottement f
de la surface agissant sur le corps sur laquelle
il se déplace est définie par f = k x R ,
où "k" est appelé le coefficient de frottement
cinétique entre le corps et la surface.
Ici R = f/ k = 0.9/0.36 = 2.5 Newtons.
R = 2.5 Newtons.
3.
a
On a : P(
F
) = W(
F
)/Δt = F x v
F la force et v la vitesse de l'objet.
P(
P
) = P x v(p) = m g sinθ v
Au point A, la puissance vaut = m g sinθ x 0 = 0.
Donc nulle.
Au point B, elle vaut = 0.5 x 10 x √3/2 x 5.24 = 22.69 W
Au point A, la puissance = 0.
Au point B, elle vaut 22.69 W
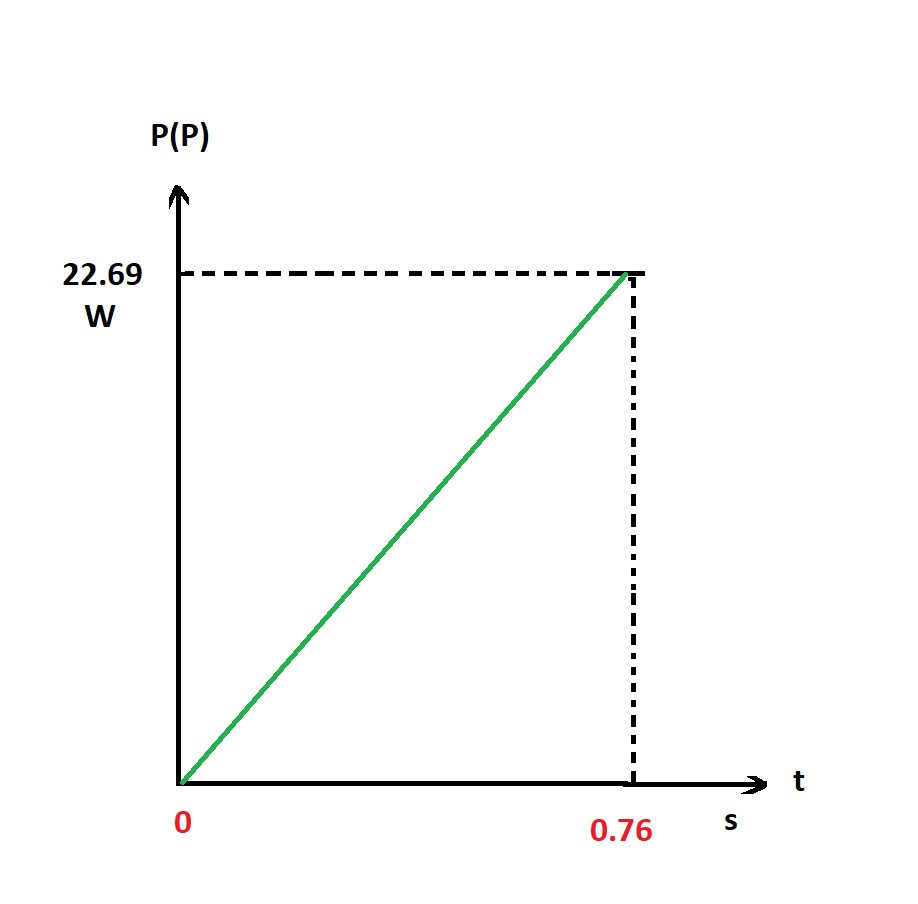
b) Si la vitesse est une fonction linéaire du temps , alors
P(
P
) l'est aussi, puisqu'ils sont proportionnels.
P(
P
) = α t
Selon le graphe:
α = P(
P
)/t = 22.69/0.76 = 29.855
α = 29.855
Nous aurons donc
P(
P
) = α t = 29.855 t
Puisque δ w(
P
)/δ t = P(
P
), alors:
δ w(
P
) = P(
P
) x δt = αt δt =
29.855 t δt
δ w(
P
) = α t δt
⇒
w(
P
)
= (1/2) α t2
= (1/2) 29.855 (0.76)2 = 8.6 Joules
w(
P
)= 8.6 Joules
Qui est la valeur
trouvée à la question 1.
Voir aussi : Sliding on frictionless surface
-- Abdurrazzak Ajaja
octobre 2023
|
|