|
Applications
© The scientific sentence. 2010
|
Least squares method
1. Interpolation and Extrapolation
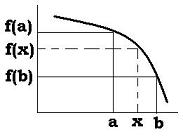
Interpolation is the process to obtain values
from an established graph or table that contain given points.
these values to find or located between these given points.
Extrapolation is the same process, but used to extend
the graph, or find values beyond the given points.
Here is the method for an interpolation:
For any functionf :
x -> f(x)
If we know the values of a and b and their results
f(a) and f(b), we can get the value of any X between
a and b:
F(X) = {[f(a) � f(b)] X + [a f(b) � b f(a)]}/(a - b)
2. The Method of Least Squares
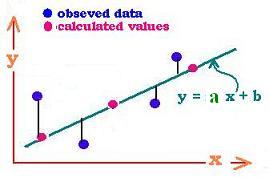 The Method of Least Squares cames from Statistics. It�s the most used method
to find the best fit line which is :
The Method of Least Squares cames from Statistics. It�s the most used method
to find the best fit line which is :
y = m xi + b.
The purpose
of this method, is to minimize the difference between the observed (yi)
and predicted values y and to determine the coefficients : m and b.
The squared quantity: (y-yi)2 may be the "least", that
is the minimum. We express this by:
dSi[(y-yi)2] /dm=0 (1) and
dSi[(y-yi)2] /db=0 (2)
(i runs from 1 to n; where n is a chosen number)
We have:
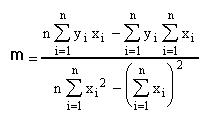 and and 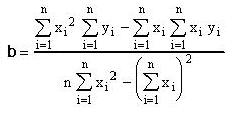
3. Example in C++ language
#include <iostream.>
#include <fstream.h>
#include <iomanip.h>
#include <ctype.>
const int maxSquares= 20;
struct Squares
{
double x, y;
};
//To make the related array :
//-------------------------
void Write(Squares square[], int &n)
{
char response;
double X,Y;
n=0;
do {
cout<<"\n\tEnter an independant variable x and an dependant
variable y: \n"<<endl;
cout<<"\t - Enter x : --> ";
cin >>X;
cout<<"\t - Enter y : --> ";
cin >>Y;
cout<<endl;
cout<<endl<<endl;
square[n].x = X;
square[n].y = Y;
cout << "\n\tIt's done. Do you want to continue?
( Y or N ) --> ";
cin >> response;
cout<<endl;
response = toupper (response);
n++;
} while(response =='Y');
}
//Function Least Squares :
//-------------------------
void squares (Squares square[], int nbSquare)
{
double S=0;
double T=0;
double P=0;
double W=0;
cout <<"\tHere is the array of the values :" << endl
<<endl;
cout <<"\t"<<setw(3) << "x"<< setw(7)
<< "y" << endl <<endl;
for(int i=0; i<nbSquare;i++)
{
cout <<"\t"<<setw(3) << square[i].x <<
setw(7) << square[i].y << endl <<endl;
S += square[i].x ;
T += square[i].y ;
P += (square[i].x)*(square[i].x);
W += (square[i].x)*(square[i].y);
}
double Slope;
Slope = (nbSquare*W - S*T)/(nbSquare*P-S*S);
double Y_intercept;
Y_intercept= (P*T - S*W)/(nbSquare*P-S*S);
cout<<"\n\t--------------------"<<endl;
cout <<"\n\tThe least squares method gives:" <<
endl <<endl;
cout<<"\n\tThe slope ( m's value) is : --->
"<<Slope<<endl;
cout<<"\n\tThe Y-intercept ( b's value) is : ---> "
<<Y_intercept<<endl;
cout<<"\n\tThen the equation of the line is : --->
"<<"y = "<<Slope<<" x + "
<< Y_intercept<<endl<<endl;
}
//Main function:
//--------------------------------
void main()
{
Squares square [maxSquares];
int nbSquares;
Write(square, nbSquares);
squares (square,nbSquares);
cout<<"\n\tThe number of points used is :
"<<nbSquares<<endl<<endl;
}
//End:-----------------------------
4. Example in C language
#include <stdio.h>
#include <math.h>
int get_number()
{
int num;
printf("\n How many points will you represent ?: --> ");
scanf("%d", &num);
return num;
}
int main()
{
int num = get_number();
float abscissas[num];
float ordinates[num];
printf("\n Enter their x_coordinates:\n");
int i;
for (i = 0; i<num; i++)
{
scanf("%f", &abscissas[i]);
}
printf("\n Enter their corresponding y_coordinates:\n");
int j;
for (j = 0; j<num ;j++)
{
scanf("%f", &ordinates[j]);
}
float x1=0.0,y1=0.0,x2=0.0,xy=0.0;
float num_slope, deno_slope, slope=0.0;
float num_intercept, deno_intercept,intercept=0.0 ;
for ( i = 0; i <= num - 1; i++)
{
x1 += abscissas[i];
y1 += ordinates[i];
x2 += abscissas[i] * abscissas[i];
xy += abscissas[i] * ordinates[i];
}
num_slope = num*xy - x1*y1;
deno_slope = num*x2 - x1*x1;
if (deno_slope == 0){
printf("\n The denominator is zero. \n");
}
else
{
slope = num_slope/deno_slope;
}
num_intercept = x2*y1 - x1*xy;
deno_intercept = num*x2 - x1*x1;
if (deno_intercept == 0){
printf("\n The denominator is zero. \n");
}
else
{
intercept = num_intercept/deno_intercept;
}
printf("\n The slope is : %2.2f, and the y_intercept
is %2.2f . \n", slope, intercept);
printf("\n");
if (intercept<0)
printf("\n The related linear equation is: y = %2.2f x
%2.2f \n", slope, intercept);
else
printf("\n The related linear equation is: y = %2.2f x +
%2.2f \n", slope, intercept);
return 0;
}
5. Example in PHP language
refer to:
Least squares with php ajax and html
|
|
|