total probability theorem
conditional probability



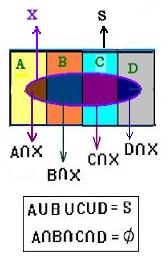
X any event,
X = (X ∩ A) ∪ (X ∩ B) ∪ (X ∩ C) ∪ (X ∩ D)

The sets (X ∩ A), (X ∩ B), (X ∩ C), and (X ∩ D) are disjoint.
Hence:
P(X) = P(X ∩ A) + P(X ∩ B) + P(X ∩ C) + P(X ∩ D)

Let's remember:
P(X ∩ Y) = P(X|Y) P(Y)
Therefore:
P(X ∩ A) = P(X|A) P(A)
P(X ∩ B) = P(X|B) P(B)
P(X ∩ C) = P(X|C) P(C)
P(X ∩ D) = P(X|D) P(D)


P(X) = P(X|A) P(A) + P(X|B) P(B)) + P(X|C) P(C)) + P(X|D) P(D) = Σ P(X|Si) P(Si)

X any event,
P(X)= Σ P(X|Si) P(Si)
Where Si is a partition of the sample space S (∩Si = Φ and ∪Si = S)