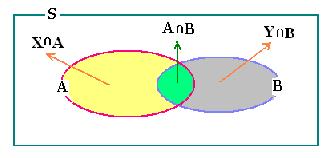
We have:
A ∪ B = (X ∩ A) ∪ (A ∩ B) ∪ (Y ∩ B)   (1)
Then:
P(A ∪ B) = P(X ∩ A) + P(A ∩ B) + P(Y ∩ B)   (1')

A = (X ∩ A) ∪ (A ∩ B)   (2)
B = (Y ∩ B) ∪ (A ∩ B)   (3)

P(A) = P(X ∩ A) + P(A ∩ B)   (2')
P(B) = P(Y ∩ B) + P(A ∩ B)   (3')

P(X ∩ A) = P(A) - P(A ∩ B)    (2")
P(Y ∩ B) = P(B) - P(A ∩ B)   (3")


P(A ∪ B) = P(X ∩ A) + P(A ∩ B) + P(Y ∩ B) (1")
= P(A) - P(A ∩ B) + P(A ∩ B) + P(B) - P(A ∩ B)
= P(A) + P(B) - P(A ∩ B)

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)