Gaussian distribution

We will set the normal distribution from 
the binomial distribution:

P(x) = n!/x!(n - x)! pxqn - x
An approximation to this binomial distribution for large n 
can be obtained by expanding about the value μ where P(x) 
is a maximum, i.e., where dP/dx=0. 

Let write x = μ + ζ and use the Maclaurin series around 
ln P(μ):

ln P(x) = ln P(μ) + ζ d/dx [ln P(x)] + (1/2)ζ2 d2/dx2[ln P(x)] + ... 

ln P(x) = ln n! - ln x! - ln (n-x)! + x ln p +(n - x) ln q

Using stirling approximation:
ln y! &asym; y ln y - y, we have:
ln P(x) = n ln n - n - x ln x! + x - (n-x) ln (n-x) + n - x + x ln p + (n - x)ln q
= n ln n - x ln x - (n-x)ln (n-x) + x ln p + (n - x)ln q
And:
d/dx [ln P(x)] = - ln x - 1 + 1 + ln(n-x) +ln p - ln q
= - ln x  + ln(n - x) + ln p - ln q

This experssion must be equal to zero, because we are developping 
around the maximum.

This condition gives us the mean:
d/dx [ln P(x)] = 0 ⇒ ln(n - x)/x = ln(q/p) 
Since p+q = 1, we have the mean = μ = np

d2/dx2[ln P(x)] = -1 /x -1/(n-x) 
With x = μ we have :

d2/dx2[ln P(x)] = -1/npq

The following terms get smaller. We can write:

ln P(x) = ln P(μ) + 0 -1/npq (1/2)ζ2, and 
P(x) = P(μ) exp {-1/2npq ζ2} 

Let' normalise this probability to 1:
∫ P(x) dx = 1 
dx = dζ
1 = ∫ P(μ) exp {-1/2npqζ2} dζ  [ζ: 0 → + ∞ ]
= (2npq)1/2 P(μ) ∫ (2npq&) exp {- ζ2} dζ
= (2npq)1/2 P(μ) (π)1/2
= (2npqπ)1/2 P(μ) 

Hence:
P(μ) = 1/(2npqπ)1/2

Thus:

P(x) = 1/(2npqπ)1/2 exp {-1/2npq ζ2} 
With:

ζ =  x - μ and σ2 = npq ,
 The Gaussian distribution:
P(x) = 1/σ(2π)1/2 exp {- (x - μ)2/σ2}
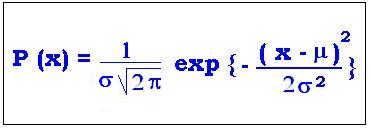