|
Leonardo's vitruvian man
Leonardo di ser Piero da Vinci (1452–1519) had drawn the vitruvian man
comming from the architect Vitruvius (Marcus Vitruvius Pollio, around the first century).
The body standing is inscribed in a square.
With feet and arms outspread, the man is inscribed in a circle.
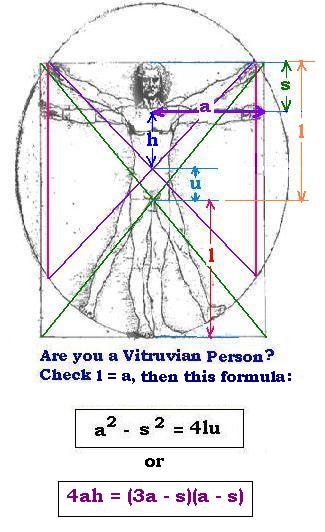
Calculations:
Using the square:
HD = diagonal/2
HD2 + HD2 = 2 HD2 = (2a)2
Hence:
HD2 = 2a2
HD2 = l2 + a2
Then:
l2 + a2 = 2a2
Hence:
l = a
Using the circle:
s2 - a2 = r2 - (l - u)2
where r is the radius of the circle.
r = l + u, then:
a2 - s2 = (l + u)2 - (l - u)2
= (l + u + l - u) x (l + u - l + u) = 2 l x 2 u = 4 ul
Hence:
a2 - s2 = 4 ul
with l = a, we have:
a2 - s2 = 4 ua
We have also:
h = l - u - s ( or a - u - s)
u = l - s - h = a - s - h
The above formula becomes:
(a + s)(a - s) = 4 a (a - s - h)
(a + s)(a - s) - 4 a (a - s - h) = 0
(a + s)(a - s) - 4 a (a - s) + 4ah = 0
4 a (a - s) - (a + s)(a - s) = 4ah
4ah = (3a - s)(a - s)
4ah = (3a - s)(a - s)
|