Mathématiques 2: Fonctions
Fonction affine
Fonction linéaire
Équation des droites

1. Définitions

L'équation d'une droite peut se mettre sous la forme:

• fonctionnelle: y = m x + n,

m est la pente de la droite, n son ordonnée à l'origine.

• générale: A x + B y + C = 0

• symétrique: x/a + y/b = 1

Par des opérations algébriques, on peut passer d'une forme à l'autre.

. De la forme générale à la forme fonctionnelle :

A x + B y + C = 0 donne y = (- A/B) x + (- C/B)

y = (- A/B) x + (- C/B)

- A/B est la pente et -C/B est l'ordonnée à l'origine.

. De la forme symétrique à la forme fonctionnelle :

x/a + y/b = 1
y/b = 1 - x/a
y = (- b/a) x + b

y = (- b/a) x + b

- b/a est la pente et b est l'ordonnée à l'origine.


Deux droites sont parallèles si et seulement si leurs pentes sont les mêmes.

Deux droites sont perpendiculaires si et seulement si le produit de leurs pentes est égal à - 1.

2. Applications

2. 1. Exercice 15

Énoncé :

Soit x/5 + y/2 = 1         (1)

l'équation d'une droite (d) .

a) Montrer que le point P(4,3) n'appartient à cette droite ?

b) Déterminer les équations de la droite parallèle à (d) et l'équation de la droite perpendiculaire à (d).

Réponse :

a) Le x du point P(4,3) est 4. Son y est 3.

En remplaçant dans l'éqution de la droite, on trouve:

4/5 + 3/2 = (8 + 15)/10 = 23/10 qui n'est pas égal à 1. Donc le point P(4,3) n'appartient à la droite (d)

b) L'équation x/5 + y/2 = 1 de la droite (d) s'ecrit sous forme fonctionnelle:

y = (- 2/5) x + 2         (2)

1) Soit y = m x + n l'équation de la droite (d1) qui passe par le point P et qui parallèle à (d).

La droite (d1) est parallèle à la droite (d). donc:

m = - 2/5

Si la droite (d1) passe par le point P, alors les coordonnées de ce point P, qui sont 4 et 3 vérifient l'équation de cette droite. Donc:

3 = 4 m + n

D'où:

n = 3 - 4m.

On remplace m par sa valeur -2/5, on trouve:

n = 3 - 4 x (- 2/5) = 3 + 8/5 = 23/5

n = 23/5

L'équation cherchée est donc:

y = - (2/5) x + 23/5


2) Soit y = p x + q l'équation de la droite (d2) qui passe par le point P et qui perpendiculaire à (d).

La droite (d2) est perpendiculaire à la droite (d). donc:

p x (-2/5) = - 1
- 2p/5 = -1

p = 5/2

Si la droite (d2) passe par le point P, alors les coordonnées de ce point P, qui sont 4 et 3 vérifient l'équation de cette droite. Donc:

3 = 4 p + q

D'où: q = 3 - 4p.

On remplace p par sa valeur 5/2, on trouve:

q = 3 - 4 x (5/2 = 3 - 10 = - 7

q = - 7

L'équaton cherchée est donc:

y = (5/2) x - 7

2. 2. Exercice 16

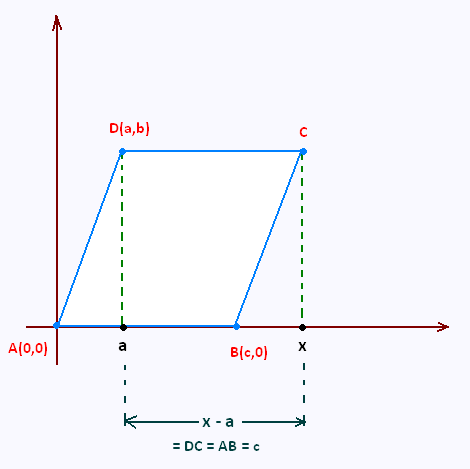
le quadrilatère ABCD est un parallélogramme, donc
(AD) // (BC) et (DC)// (AB).

De plus AD = BC et DC = AB

Le point D a pour abscisse a et pour ordonnée b.

Si (DC) //(AB), c'est à dire (DC)// l'axe des x, alors
l'ordonnée du point C est b .

Le point D a pour abscisse a.
AB = c.
Si x est l'abscisse de C, alors x - a = DC = AB = c

x - a = c. d'où: x = a + c

Ainsi, le point C a pour abscisse a + c et pour odonnée b.

C(a + c, b)


b) • Équation de la droite (AC).

La droite (AC) passe par l'origine donc son équation prend la forme: y = m x

Le point C est sur cette droite, il vérifie donc cette équation:

b = m (a + c). D'où:

m = b/(a + c)

L'équation de la droite (AC) est donc:

y = [b/(a + c)] x

• Équation de la droite (BD).

La droite (BD) a pour équation

y = p x + q

. Le point B(c,0) est sur cette droite, il vérifie donc cette équation:

0 = p c + q . D'où:

q = - p c

. Le point D(a, b) est sur cette droite, il vérifie donc cette équation:

b = p a + q .

On remplace q par sa valeur:

b = p a - p c = p(a - c). D'où

p = b/(a - c)

On remplace p par sa valeur:

q = - b/(a - c) x c = - bc/(a - c)

q = - bc/(a - c)

L'équation de la droite (BD) est donc:

y = [b/(a - c)] x - bc/(a - c)

• La droite (BD) est perpendiculaire à (AC) donc:

[b/(a + c)] x [b/(a - c)] = - 1

b² = - (a + c)(a - c) = c² - a²

a² + b² = c²

Telle est la relation cherchée.


c) On utilise la formule de la distance:

d(A,B) = √[(c - 0)² + (0 - 0)²] = c

d(A,B) = c

d(A,D) = √[(a - 0)² + (b - 0)²] =
√[a² + a²]

D'après la relation trouvée en b), a² + b² = c² , on a donc:

d(A,D) = √[a² + a²] = √[c²] = c

d(A,D) = c

On obtient donc:

d(A,B) = c, et
d(A,D) = c

D'où:

d(A,B) = d(A,D)

AB = AD

Conclusion:

le quadrilatère ABCD est un parallélogramme
On vient de démontrer que AB = AD.
Donc
le quadrilatère ABCD est donc un losange.
d'après la définition :
Un losange est un parallélogramme ayant deux côtés consécutifs de même longueur.

2. 3. Exercice 17

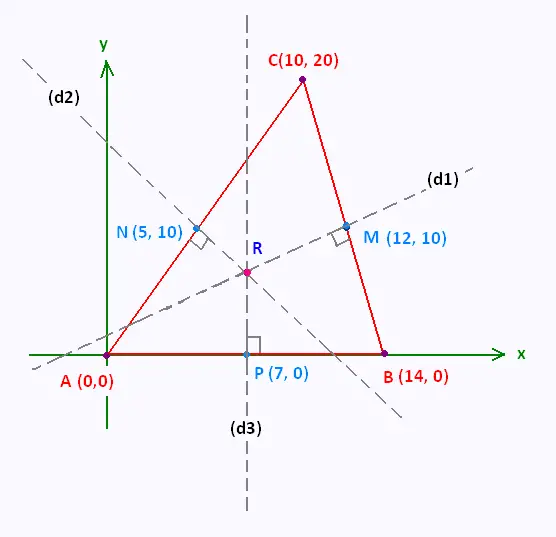
Les médiatrices d'un triangle quelconque se rencontrent en un point qui est le centre du cercle circonscrit au triangle. Ce point est donc à égale distance des sommets du triangle.

On veut vérifier cette propriété à l'aide du triangle ABC représenté sur un plan cartésien (xOy).

a) Médiatrice des droites (d1), (d2) et (d3):

• Médiatrice de la droite (d1):

On détermine d'abord l'équation de la droite (BC). Soit y = a x + b cette équation.

Cette droite passe par les points B(14,0) et C(10,20). Ces deux points vérifient donc l'équation y = a x + b.

Donc:

0 = 14 a + b → b = - 14 a
20 = 10 a + b → 20 = 10 a - 14 a = - 4 a → a = 20/(- 4) = - 5

D'où

b = - 14 x (- 5) = 70

a = - 5
b = 70

L'équation de la droite (BC) est donc :

y = - 5 x + 70

Soit y = m x + n l'équation de la droite médiatrice (d1). Cette droite (d1) est perpendiculaire à (BC). D'où:

m x (- 5) = - 1 → m = 1/5

L'équation de la droite médiatrice (d1) devient:

y = (1/5) x + n

Les coordonnées du point M mlieu du côté [B,C] sont

(14 + 10)/2 = 12 pour abcsisse, et
(0 + 20)/2 = 10 pour ordonnée.

Donc:

M(12, 10)

De plus le point M est sur la droite (d1). Il vérifie donc l'équation de cette droite, soit:

10 = (1/5) x (12) + n = 12/5 + n → n = 10 - 12/5 =
(50 - 12)/5 = 38/5

n = 38/5

L'équation de la droite médiatrice (d1) s'ecrit enfin:

y = (1/5) x + 38/5


• Médiatrice de la droite (d2):

On détermine d'abord l'équation de la droite (AC).

Cette droite (AC) passe par l'origine O. Son équation est donc de la forme y = a x.

Cette droite passe par le point C(10,20). Ce point vérifie donc l'équation y = a x .

Donc:

20 = 10 a → a = 20/10 = 2

a = 2

L'équation de la droite (AC) est donc :

y = 2 x

Soit y = m x + n l'équation de la droite médiatrice (d2). Cette droite (d2) est perpendiculaire à (AC). D'où:

m x (2) = - 1 → m = - 1/2

L'équation de la droite médiatrice (d2) devient:

y = - (1/2) x + n

Les coordonnées du point N mlieu du côté [A,C] sont;

(0 + 10)/2 = 5 pour abcsisse, et
(0 + 20)/2 = 10 pour ordonnée.

Donc:

N(5, 10)

De plus le point N est sur la droite (d2). Il vérifie donc l'équation de cette droite, soit:

10 = (- 1/2) x (5) + n = - 5/2 + n → n = 10 + 5/2 = 25/2

n = 25/2

L'équation de la droite médiatrice (d2) s'ecrit enfin:

y = - (1/2) x + 25/2


• Médiatrice de la droite (d3):

Les coordonnées du point P mlieu du côté [A,B] sont:

(0 + 14)/2 = 7 pour abcsisse, et
(0 + 0)/2 = 0 pour ordonnée.

Donc:

P(7, 0)

La droite (d3) est parallèle l'axe des ordonnées. Son équation est donc simplement x = 7.

L'équation de la droite (d3) est donc :

x = 7

Resumé:

(d1): y = (1/5) x + 38/5
(d2): y = - (1/2) x + 25/2
(d3): x = 7


b) Quel sont donc les coordonnées du point de rencontre R ?

Les coordonnées (xo, yo) de ce point R doivent vérifier les trois équations des droites (d1), (d2) et (d3) en même temps. Soit:

xo = 7

On remplace cette valeur dans l'une ou l'autres des équations de (d1) ou (d2). Dans (d1), on a

yo = (1/5) xo + 38/5 = (1/5) x (7) + 38/5 =
(7 + 38)/5 = 45/7 = 9

yo = 9

Les coordonnées du point de rencontre R sont xo = 7 , yo = 9.

R(7, 9)


c) On applique la formule des distances:

Nous vaons:

A(0,0), B(14,0), C(10,20), et R(7, 9),

Donc:

d(R,A) = √[(0 - 7)² + (0 - 9)²] =
√[(7)² + (9)²] = √130.

d(R,B) = √[(14 - 7)² + (0 - 9)²] =
√[(7)² + (9)²] = √130.

d(R,C) = √[(10 - 7)² + (20 - 9)²] =
√[(3)² + (11)²] = √(9 + 121) = √130.

Ainsi, les trois distances sont égales.

d(R,A) = d(R,B) = d(R,C)

Le point R est donc à égal distance des sommets tu triangle ABC.

On vérifie donc la propriété:

« Les médiatrices d'un triangle quelconque se rencontrent en un point à égale distance des sommets du triangle.»

2. 4. Exercice 18

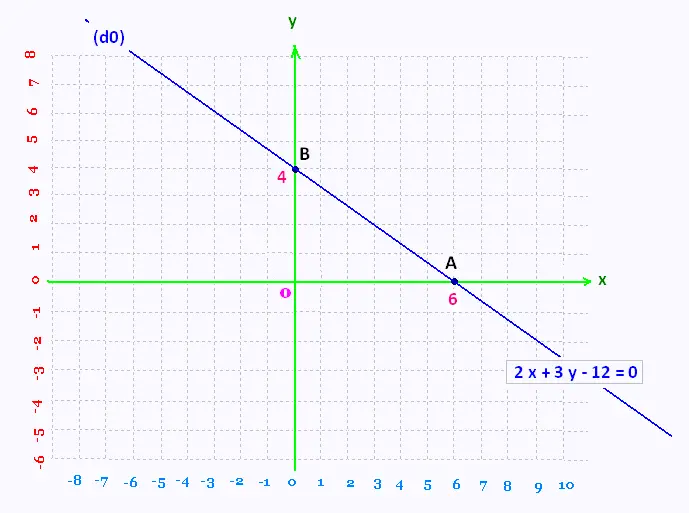
L'équation, ecrite sous forme générale, de la droite (d0) est

2 x + 3 y - 12 = 0

Sur un plan cartésien, le point A sur cette droite a pour coordonnées (6, 0). Le point B (0, 4).

a)

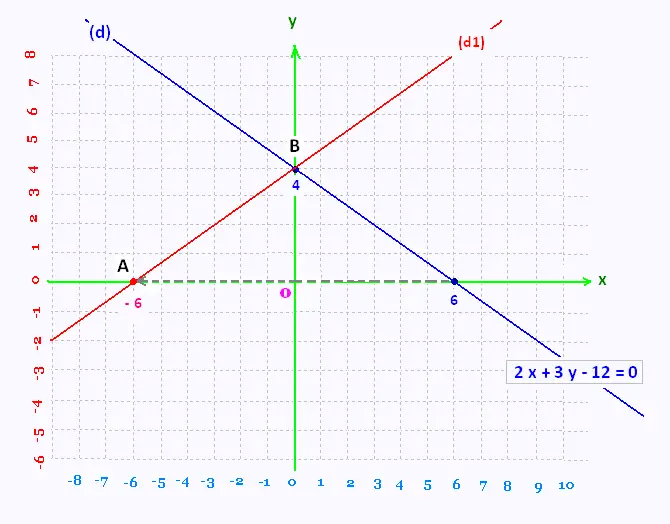
Une réflexion par rapport à l'axe de y laisse le point B immobile et glisse le point A horizontalement de + 6 à - 6.

Soit (d1) la nouvelle droite, image de la droite (d0) par cette transformation. y = a x + b son équation.

Les point A(- 6,0) et B(0,4) appartiennent à cette nouvelle droite (d1). Ils vérifient donc l'équation y = a x + b. Soit:

0 = - 6 a + b → a = b/6
4 = 0 a + b → b = 4

Donc

a = 4/6 = 2/3

a = 2/3, b = 4

L'équation de la droite (d1) est donc:

y = (2/3) x + 4

Sous forme générale,

y - 2 x/3 - 4 = 0
- 2 x + 3 y - 12 = 0

(d1) : - 2 x + 3 y - 12 = 0




b)

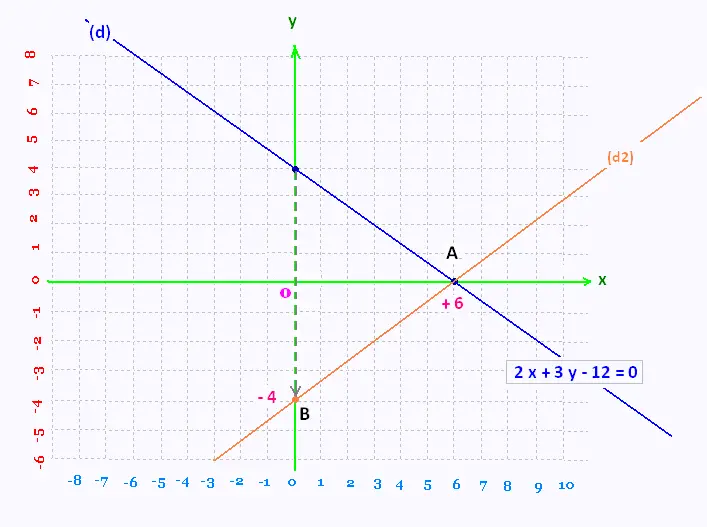
Une réflexion par rapport à l'axe de x laisse le point A inchangé et déplace le point B verticalement de + 4 à - 4 .

Soit (d2) la nouvelle droite, image de la droite (d0) par cette transformation. y = a x + b son équation.

Les point A(6,0) et B(0,- 4) appartiennent à cette nouvelle droite (d2). Ils vérifient donc l'équation y = a x + b. Soit:

0 = 6 a + b → a = - b/6
- 4 = 0 a + b → b = - 4

Donc

a = 4/6 = 2/3

a = 2/3, b = - 4

L'équation de la droite (d2) est donc:

y = (2/3) x - 4

Sous forme générale,

y - 2 x/3 + 4 = 0
- 2 x + 3 y + 12 = 0

(d2) : - 2 x + 3 y + 12 = 0


c)

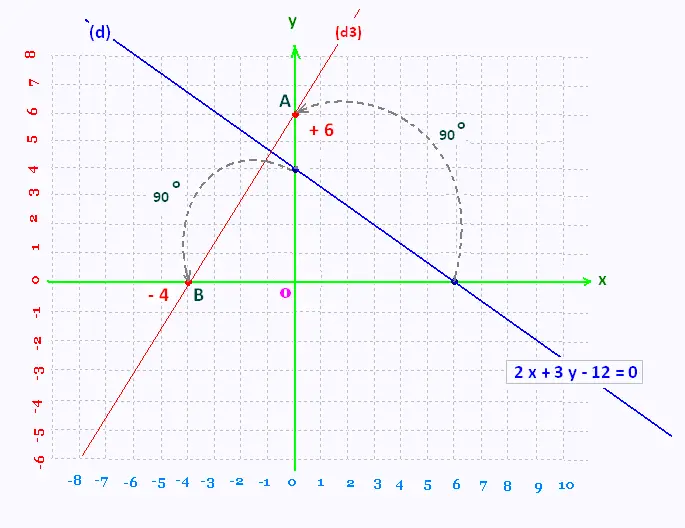
Une rotation de 90^o autour de l'origine déplace les points A et B d'un quart de tour vers la gauche. A devient A((0, 6) et B(- 4, 0).

Soit (d3) la nouvelle droite, image de la droite (d0) par cette transformation. y = a x + b son équation.

Les point A(0,6) et B(- 4,0) appartiennent à cette nouvelle droite (d3). Ils vérifient donc l'équation y = a x + b. Soit:

6 = 0 a + b → b = 6
0 = (- 4) a + b → 4 a = b → a = b/4 = 6/4 = 3/2

Donc:

a = 3/2, b = 4

L'équation de la droite (d3) est donc:

y = (3/2) x + 4

Sous forme générale,

y - 3 x/2 - 4 = 0
- 3 x + 2 y - 8 = 0

(d3) : - 3 x + 2 y - 8 = 0




d)

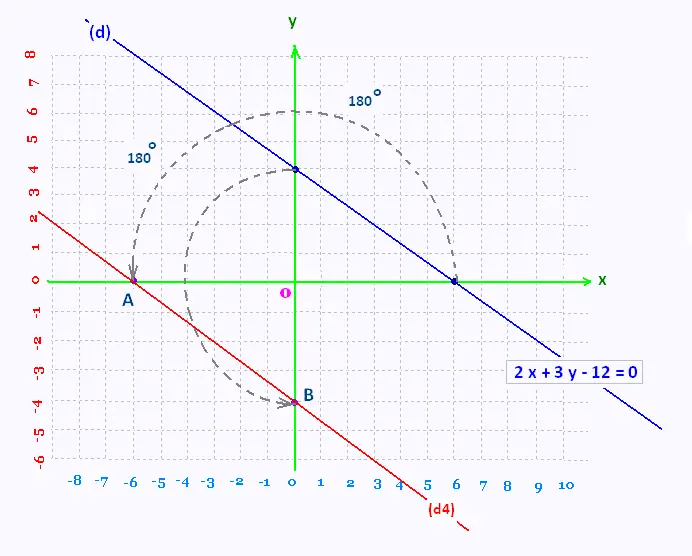
Une rotation de 180^o autour de l'origine déplace les points A et B d'un demi-tour dans le sens trigonométrique. A devient A((-6, 0) et B(- 4, 0).

Soit (d4) la nouvelle droite, image de la droite (d0) par cette transformation. y = a x + b son équation.

Les point A(-6,0) et B(0,- 4) appartiennent à cette nouvelle droite (d4). Ils vérifient donc l'équation y = a x + b. Soit:

0 = - 6 a + b → a = b/6
- 4 = 0 a + b → b = - 4

D'où: a = - 4/6 = - 2/3

Donc

a = - 2/3, b = - 4

L'équation de la droite (d4) est donc:

y = - (2/3) x - 4

Sous forme générale,

y + 2x/3 + 4 = 0
2 x + 3 y + 12 = 0

(d4) : 2 x + 3 y + 12 = 0