Maths
- 2 -
Fonctions
© The scientific sentence. 2010
| |
Mathématiques 2:
Analyse des fonctions linéaires et quadratiques
1. La méthode
Pour analyser une fonction, on determine:
- Son domaine de définition,
- Son codomain ou image,
- Ses axes de symétrie,
- Ses asymptotes,
- Ses zéros,
- Son ordonnée à l'origine,
- Sa croissance/décroissance,
- Ses signs, et
- Ses extremums.
2. Exemples
2.1. Exemple 1: 2y - 3x - 7 = 0
2y - 3x - 7 = 0
y = (3/2)x + 7/2
Dom = R
Codom = Image = R
Axes de symétrie: Aucun
asymptotes: Aucune
Zéros x = - 7/3
ordonnée à l'origine: y = 7/2
croissance: Δy/Δx = +3/2 > 0 →
fonction croissante
signs:
y >0 si (3/2)x + 7/2 > → x > - 7/3 : ]-7/3, + ∞[
y <0 si (3/2)x + 7/2 < → x < - 7/3 : ]- ∞, - 7/3[
Extremums: Aucun.
Graphique :
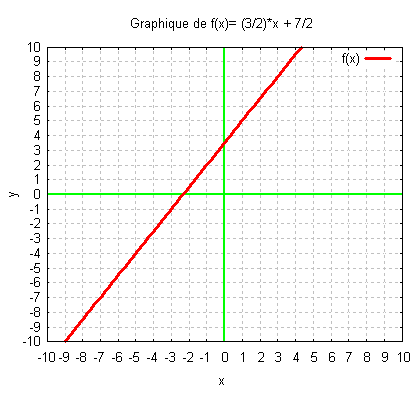
2.2. Exemple 2: y = - 3 x2 + 4 x - 5
y = - 3 x2 + 4 x - 5
Dom = R
Codom = Image = R
Axes de symétrie:
On cherche deux x : x1 et x2 qui ont un même y et
puis on divise par 2.
x1 = 0 → f(0) = - 5 (Eq.1)
- 3 x22 + 4 x2 - 5 = - 5
(Eq.2)
Egalisons le deux équations, onobtient:
x2(4 - 3 x2) = 0
Donc x2 = 0 ou 4/3
Symetrie est l'axe x = (0 + 4/3)/2 = 2/3
asymptotes: Aucune
Zéros x = Aucun
ordonnée à l'origine: y = - 5
croissance:
croissante dans : ]- ∞, 2/3[
décroissante dans ]2/3, + ∞[
signs:
f(x) <0 partout dans son Dom.
Extremums: Minimum (x = 2/3, y = -5).
Graphique:
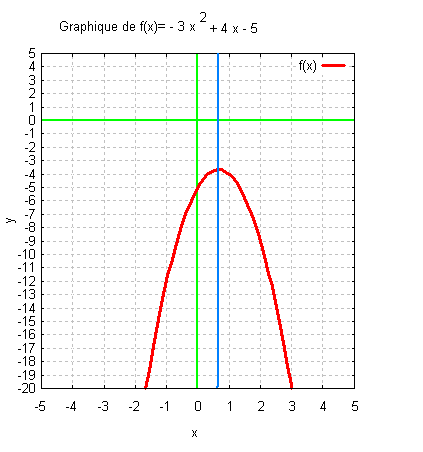
|
|