Maths
- 2 -
Fonctions
© The scientific sentence. 2010
| |
Mathématiques 2: Fonctions rationnelles
1. Fonction rationnelle de base
La fonction rationnelle de base est la fomction
qui correspond à une situation de proportionnalité
inverse. Elle s'ecrit:
f(x) = 1/x
Son graphe est:
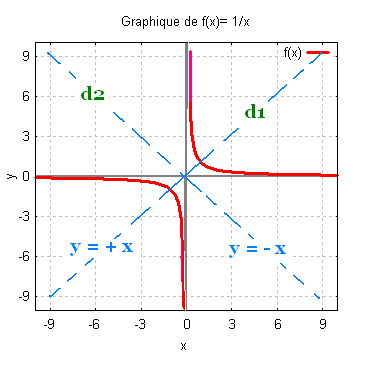 La fonction rationnelle de base est une fonction
discontinue en 0. Son domaine est R\{0} ou R*
et son codomaine est aussi R*. Elle possède
deux axes de symétrie qui sont des droites d1 d'équation
y = x et d2 d'équation y = - x.
La fonction rationnelle de base est une fonction
discontinue en 0. Son domaine est R\{0} ou R*
et son codomaine est aussi R*. Elle possède
deux axes de symétrie qui sont des droites d1 d'équation
y = x et d2 d'équation y = - x.
2. Fonction homographique
Une fonction rationnelle de la forme
y = (a x + b)/(c x + d)
ou de la forme transformée:
y = a/b(x - h) + k
est dite fonction homographique.
Le graphique de cette fonction possède deux
séparations:
La droite verticale correspond à la valeur qui annule
le dénominateur .
La droite horizontale correspond à la valeur
de y lorsque x tend vers l’infini.
Ces deux droites sont appelées des asymptotes.
La courbe s’approche de plus en plus de la droite
asymptotique lorsque x se rapproche de l’infini sans
jamais l’atteindre ni la traverser.
Le domaine de définition de la fonction
homographique Dom = R\{h}. Son codomaine
est Codom = R\{k}
3. Exemple:
y = 2/(x - 3) + 4
h = 3, k = 4, Dom = R\{3}, Codom = R\{4}.
La droite d'équation x = 3 est l'asymptote
verticale.
La droite d'équation y = 4 est l'asymptote
horizontale.
Son graphique est:
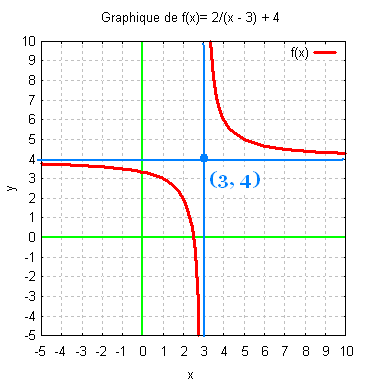
4. Equations et Inéquations
Exemple 1
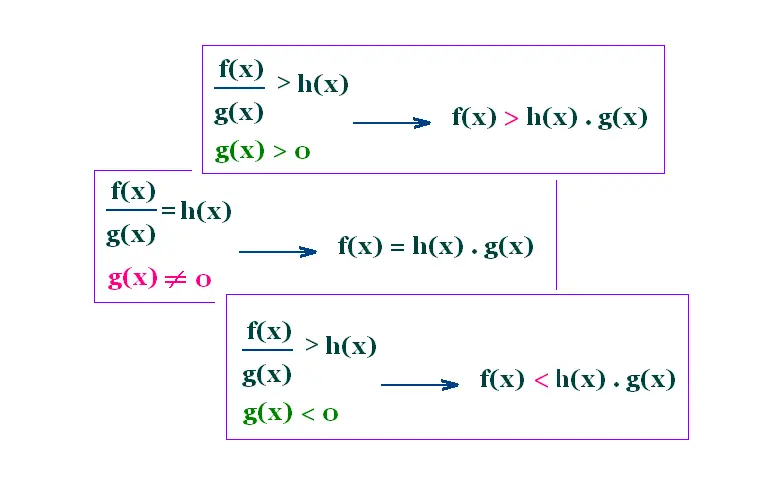 f(x) = 7/(x - 3) ≥ 4
i) si x - 3 > 0 ou x > 3 , a;ors
7 ≥ 4 . (x - 3)
7 ≥ 4 x - 12
4 x ≤ 19
x ≤ 19/4
Ainsi : Il faut que x ≤ 19/4 avec x > 3
l'ensemble des solutions est S1 = ]3, 19/4]
f(x) = 7/(x - 3) ≥ 4
i) si x - 3 > 0 ou x > 3 , a;ors
7 ≥ 4 . (x - 3)
7 ≥ 4 x - 12
4 x ≤ 19
x ≤ 19/4
Ainsi : Il faut que x ≤ 19/4 avec x > 3
l'ensemble des solutions est S1 = ]3, 19/4]
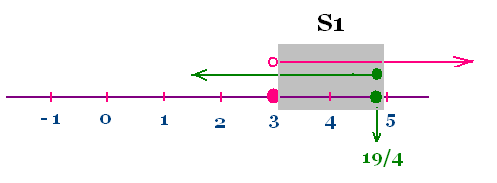 2) si x - 3 < 0 ou x < 3 , alors
7 ≤ 4 . (x - 3)
7 ≤ 4 x - 12
4 x ≥ 19
2) si x - 3 < 0 ou x < 3 , alors
7 ≤ 4 . (x - 3)
7 ≤ 4 x - 12
4 x ≥ 19
 x ≥ 19/4
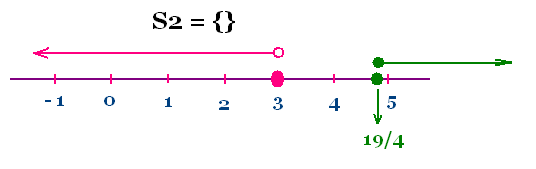
Ainsi : Il faut que x ≥ 19/4 avec x < 3 ,
ce qui est impossible: S = Φ
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = ]3, 19/4] ∪ Φ = ]3, 19/4]
x ≥ 19/4
Ainsi : Il faut que x ≥ 19/4 avec x < 3 ,
ce qui est impossible: S = Φ
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = ]3, 19/4] ∪ Φ = ]3, 19/4]
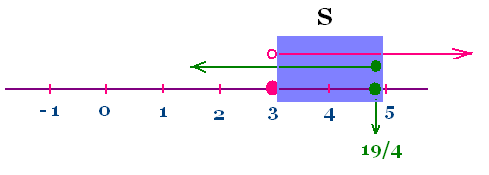 S = ]3, 19/4]
S = ]3, 19/4]
Exemple 2
(x + 2)/(3 x - 4) ≥ 3 x - 8
1) 3 x - 4 > 0 ou x > 4/3 :
x + 2 ≥ (3 x - 8)(3 x - 4)
x + 2 ≥ 9x2 -12 x -24 x + 32
0 ≥ 9x2 - 37 x + 30
0 ≥ 9(x - 10/9)(x - 3)
Le coefficient 9 de x2 est positif, Ce
trinôme est negatif à l'interieur des racines
x1 = 3 et x2 = 10/9, c'est à dire dans
l'intervalle [10/9, 3].
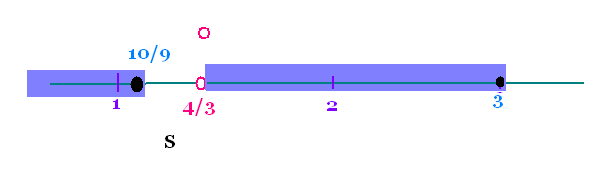
10/9 = 1.111, 4/3 = 1.333 , donc 4/3 > 10/9
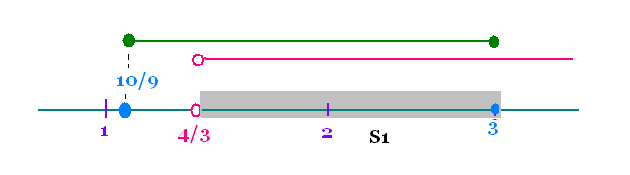 Avec x > 4/3, on a:
L'ensemble des solutions est S1 = ]4/3, 3].
2) 3 x - 4 < 0 ou x < 4/3 :
x + 2 ≤ (3 x - 8)(3 x - 4)
x + 2 ≤ 9x2 -12 x -24 x + 32
0 ≤ 9x2 - 37 x + 30
0 ≤ 9(x - 10/9)(x - 3)
Le coefficient 9 de x2 est positif, Ce
trinôme est positif à l'extérieur des racines
x1 = 3 et x2 = 10/9, c'est à dire dans
l'intervalle ]- ∞, 10/9] ∪ [3, + ∞[ .
Avec x > 4/3, on a:
L'ensemble des solutions est S1 = ]4/3, 3].
2) 3 x - 4 < 0 ou x < 4/3 :
x + 2 ≤ (3 x - 8)(3 x - 4)
x + 2 ≤ 9x2 -12 x -24 x + 32
0 ≤ 9x2 - 37 x + 30
0 ≤ 9(x - 10/9)(x - 3)
Le coefficient 9 de x2 est positif, Ce
trinôme est positif à l'extérieur des racines
x1 = 3 et x2 = 10/9, c'est à dire dans
l'intervalle ]- ∞, 10/9] ∪ [3, + ∞[ .
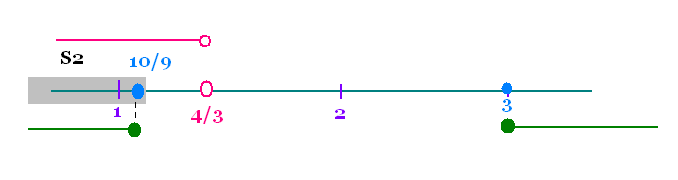 Avec x < 4/3, on a:
L'ensemble des solutions est S2 = ]- ∞, 10/9] .
Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = ]4/3, 3] ∪ ]- ∞, 10/9] =
]- ∞, 10/9] ∪ ]4/3, 3].
Avec x < 4/3, on a:
L'ensemble des solutions est S2 = ]- ∞, 10/9] .
Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = ]4/3, 3] ∪ ]- ∞, 10/9] =
]- ∞, 10/9] ∪ ]4/3, 3].
Exemple 3
(2x - 9)/(11 x + 3) > 12
1) 11 x + 3 > 0, x > - 3/11
2x - 9 > 12 (11 x + 3)
2x - 9 > 132 x + 36
0 > 130 x + 45
0 > 26 x + 9
x < - 9/26
- 9/26 = - 0.35, - 3/11 = - 0.27, donc: - 9/26 < - 3/11
Pas de solutions: S1 = Φ
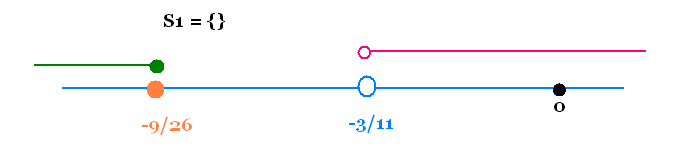 2) 11 x + 3 < 0, x < - 3/11
2x - 9 < 12 (11 x + 3)
2x - 9 < 132 x + 36
0 < 130 x + 45
0 < 26 x + 9
x > - 9/26
L'ensemble des solutions est : S2 = [-9/26, -3/11[
2) 11 x + 3 < 0, x < - 3/11
2x - 9 < 12 (11 x + 3)
2x - 9 < 132 x + 36
0 < 130 x + 45
0 < 26 x + 9
x > - 9/26
L'ensemble des solutions est : S2 = [-9/26, -3/11[
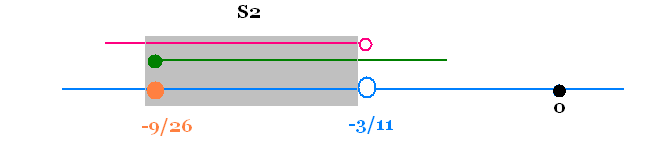 Ainsi,
L'ensemble des solution de l'inégalité donnée est
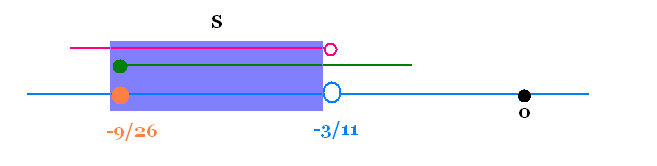
S = S1 ∪ S2 = Φ ∪ [-9/26, -3/11[ =
[-9/26, -3/11[.
Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = Φ ∪ [-9/26, -3/11[ =
[-9/26, -3/11[.
Exemple 4
- 3 ≤ (3 x - 1)/4x ≤ 9
Nous avons deux inequations:
- 3 ≤ (3 x - 1)/4x (1)
(3 x - 1)/4x ≤ 9 (2)
1) Equation (1):
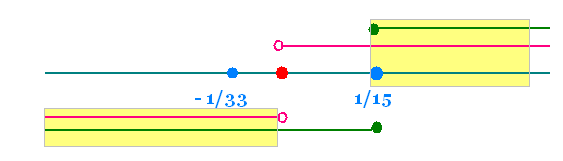
a) x > 0 : - 12x ≤ 3 x - 1, 1 ≤ 15 x, x ≥ 1/15
b) x < 0 : - 12x ≥ 3 x - 1, 1 ≥ 15 x, x ≤ 1/15
S1 = ]- ∞, 0] ∪ [1/15, +∞[
 2) Equation (2):
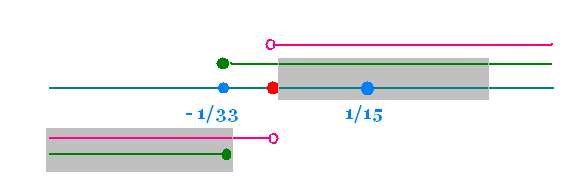
a) x > 0 : 3 x - 1 ≤ 36x - 1 ≤ 33 x , x ≥ - 1/33
b) x < 0 : 3 x - 1 ≥ 36x - 1 ≥ 33 x , x ≤ - 1/33
S2 = ]- ∞, -1/33] ∪ [0, +∞[
2) Equation (2):
a) x > 0 : 3 x - 1 ≤ 36x - 1 ≤ 33 x , x ≥ - 1/33
b) x < 0 : 3 x - 1 ≥ 36x - 1 ≥ 33 x , x ≤ - 1/33
S2 = ]- ∞, -1/33] ∪ [0, +∞[
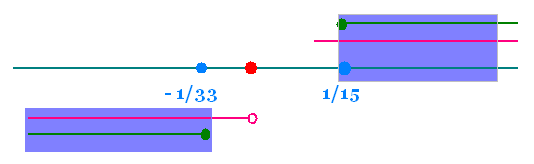
 Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∩ S2 = ]- ∞, 0] ∪ [1/15, +∞[ ∩ ]- ∞, -1/33] ∪ [0, +∞[ =
]- ∞, - 1/33]∪ [1/15, +∞[.
Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∩ S2 = ]- ∞, 0] ∪ [1/15, +∞[ ∩ ]- ∞, -1/33] ∪ [0, +∞[ =
]- ∞, - 1/33]∪ [1/15, +∞[.
Exemple 5
(5x + 7)/(- 9x + 7) < x - 8
1) - 9x + 7 > 0, - 9x > -7, 9x < 7, x < 7/9
5x + 7 < (x - 8)(- 9x + 7)
5x + 7 < - 9x2 + 7x + 72 x - 56
0 < - 9x2 + 74 x - 63
0 > 9x2 - 74 x + 63 (Inéqu. 1)
Δ' = (- 37)2 - (9)(63) = 1369 - 567 = 802
= (28.32)2
x1 = (37 - 28.32)/9 = 0.96
x2 = (37 + 28.32)/9 = 7.26
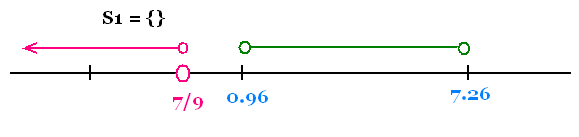
Le coefficient du trinôme 9x2 - 74 x + 63
est positif. Ce trinôme est < 0 à l'intérieur des
racines, c'est à dire dans ]0.96, 7.26[. Avec la
contrainte x < 7/9 = 0.78 , l'ensemble des
solutions de l'inéquation (Inéqu. 1) est S1 = Φ.
 2) x > 7/9
5x + 7 > (x - 8)(- 9x + 7)
0 < 9x2 - 74 x + 63 (Inéqu. 2)
Le coefficient du trinôme 9x2 - 74 x + 63
est positif. Ce trinôme est > 0 à l'extérieur des
racines, c'est à dire dans ]- ∞, 0.96[ ∪ ] 7.26, + ∞[.
Avec la contrainte x > 7/9 = 0.78 , l'ensemble
des solutions de l'inéquation (Inéqu. 2) est
S2 = ]- 7/9, 0.96[ ∪ ]7.26, + ∞[.
2) x > 7/9
5x + 7 > (x - 8)(- 9x + 7)
0 < 9x2 - 74 x + 63 (Inéqu. 2)
Le coefficient du trinôme 9x2 - 74 x + 63
est positif. Ce trinôme est > 0 à l'extérieur des
racines, c'est à dire dans ]- ∞, 0.96[ ∪ ] 7.26, + ∞[.
Avec la contrainte x > 7/9 = 0.78 , l'ensemble
des solutions de l'inéquation (Inéqu. 2) est
S2 = ]- 7/9, 0.96[ ∪ ]7.26, + ∞[.
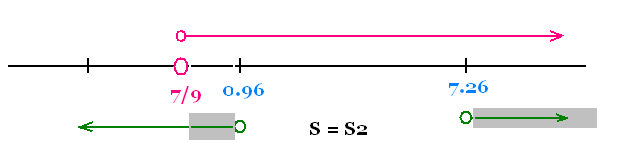 Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = S2 = ]- 7/9, 0.96[ ∪ ]7.26, + ∞[.
Ainsi,
L'ensemble des solution de l'inégalité donnée est
S = S1 ∪ S2 = S2 = ]- 7/9, 0.96[ ∪ ]7.26, + ∞[.
Exemple 6
(x + 6)/(3x + 7) ≥ (- 4x + 1)/(5x)
(x + 6)/(3x + 7) - (- 4x + 1)/(5x) ≥ 0
[(5x)(x + 6) + (3x + 7)(4x - 1)]/(5x)(3x + 7) ≥ 0
(17 x2 + 55 x - 7)/(5x)(3x + 7) ≥ 0
Δ = (55)2 - 4 (17)(-7) = (59.2)2
x1 = (- 55 - 59.2)/34 = - 3.36
x2 = (- 55 + 59.2)/34 = 0.11
(17 x2 + 55 x - 7) = 17(x + 3.36 )(x - 0.11)
L'inéquation devient:
f(x) = 17(x + 3.36 )(x - 0.11)/(5x)(3x + 7) ≥ 0
- 7/3 = - 2.33
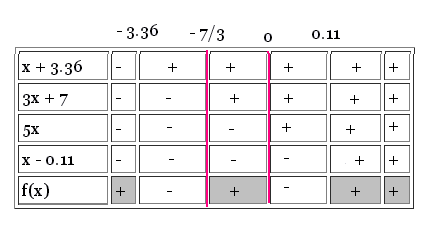 S = ]- ∞, -3.36 ] ∪ ]- 7/3, 0[ ∪ [0.11, + ∞[.
S = ]- ∞, -3.36 ] ∪ ]- 7/3, 0[ ∪ [0.11, + ∞[.
Exemple 7
10 ≤ (3 x + 4)/(x2 + 5 x)
0 ≤ (3 x + 4)/(x2 + 5 x) - 10 =
(3 x + 4 - 10 x2 - 50 x)/(x2 + 5 x) =
(- 10 x2 - 47 x + 4)/(x2 + 5 x)
L'inéquation devient:
0 ≤ (- 10 x2 - 47 x + 4 )/(x2 + 5 x), ou
0 ≥ (10 x2 + 47 x - 4)/(x2 + 5 x) = f(x)
Pour le trinôme: 10 x2 + 47 x - 4
Δ = (47)2 - 4 (10) (- 4) = (47)2 + 160 = 2369 =
(48.67)2
Les racines sont:
x1 = (- 47 - 48.67)/20 = - 4.8
x2 = (- 47 + 48.67)/20 = + 0.08
Pour x2 + 5 x = x(x + 5)
Les racines sont:
x3 = 0
x4 = - 5
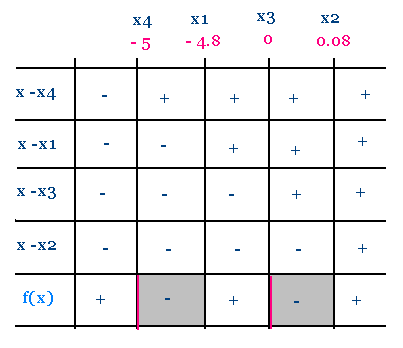 On veut que f(x) soit négative, donc
l'ensembles des solutions de l'inéquation
donnée est :
S = ]- 5, -4.8] ∪ ]0, 0.08].
On veut que f(x) soit négative, donc
l'ensembles des solutions de l'inéquation
donnée est :
S = ]- 5, -4.8] ∪ ]0, 0.08].
Exemple 7
(12 x + 8)/(3 - 5 x) ≥ |2x - 7| + 1 (1)
L'équation (1) peut s'ecrire:
(12 x + 8)/(3 - 5 x) -1 ≥ |2x - 7|
(17 x + 5)/(3 - 5 x) ≥ |2x - 7| (2)
0) Il faut tout d'abord que (17 x + 5)/(3 - 5 x)
soit positif: (17 x + 5)/(3 - 5 x) ≥ 0 avec
(3 - 5 x) ≠ 0, c'est à dire x ≠ 3/5.
Les racines des monômes (12 x + 8) et (3 - 5 x) sont
x01 = - 5/17 = - 0.294 et x02 = + 3/5 = + 0.6
Donc (12 x + 8)/(5 x - 3) < 0 à l'intérieur des
racines; c'est à dire dans [- 5/17, 3/5[
L'ensemble des slutions doit donc être contenu
dans S0 = [- 5/17, 3/5[
L'équation (1') peut s'ecrire comme une double
inéquation:
- (17 x + 5)/(3 - 5 x) ≤ 2x - 7 ≤ (17 x + 5)/(3 - 5 x)
C'est à dire:
- (17 x + 5)/(3 - 5 x) ≤ 2x - 7 (3)
d'ensemble de solution S1, et
2x - 7 ≤ (17 x + 5)/(3 - 5 x) (4)
d'ensemble de solution S2.
1)
On s'occupe d'abord de l'inéquation (3)
- (17 x + 5)/(3 - 5 x) ≤ 2x - 7 (3)
a) Si 3 - 5x > 0, x < 3/5, alors
l'inéquation (3) s'ecrit:
- (17 x + 5) ≤ (2x - 7)(3 - 5 x) = - 10 x2 + 41 x - 21
0 ≤ - 10 x2 + 41 x - 21 + 17 x + 5 = - 10 x2 + 58 x - 16
ou
0 ≥ 5x2 - 29 x + 8
Δ = (29)2 - 4(5)(8) =
681 = (26.1)2
x1 = (29 + 26.1)/10 = + 5.51
x2 = (29 - 26.1)/10 = + 0.29
Le trinôme 5x2 - 29 x + 8 est negatif ou nul
à l'intérieur des racines x1 et x2, donc
dans [0.29, 5.51]. Avec la contrainte x < 3/5 = 0.6,
l'ensemble des solutions se réduit à S1a = [0.29, 0.6[.
b) Maintenant si 3 - 5x < 0, x > 3/5, alors
l'inéquation (3) s'ecrit:
- (17 x + 5) ≥ (2x - 7)(3 - 5 x) = - 10 x2 + 41 x - 21
0 ≥ - 10 x2 + 41 x - 21 + 17 x + 5 = - 10 x2 + 58 x - 16
ou
0 ≤ 5x2 - 29 x + 8
Le trinôme 5x2 - 29 x + 8 est positif ou nul
à l'extérieur des racines x1 et x2, donc
dans ]- ∞ 0.29] ∪ [5.51, + ∞[.
Avec la contrainte x > 3/5 = 0.6,
l'ensemble des solutions se réduit à S1b = [5.51, + ∞[.
Ainsi, l'ensemble des solutions de l'inéquation (3)
est S1 = S1a ∪ S1b = [0.29, 0.6[ ∪ [5.51, + ∞[.
S1 = [0.29, 0.6[ ∪ [5.51, + ∞[
2)
On s'occupe d'abord de l'inéquation (4)
2x - 7 ≤ (17 x + 5)/(3 - 5 x) (4)
a) Si 3 - 5x > 0, x < 3/5, alors
l'inéquation (4) s'ecrit:
(17 x + 5) ≥ (2x - 7)(3 - 5 x) = - 10 x2 + 41 x - 21
0 ≥ - 10 x2 + 41 x - 21 - 17 x - 5 = - 10 x2 + 24 x - 26
ou
0 ≤ 5x2 - 12 x + 13
Δ' = (- 6)2 - (5)(13) = 36 - 65 = - 29.
Ce discriminant est négatif, donc le trinôme 5x2 - 12 x + 13
n' a pas de racines. Il est toujous postif. L'ensemble
des solutions est R. Avec la contrainte x < 3/5,
l'ensemble des solutions se réduit à S1b = ]- ∞, 0.6[.
b) Maintenant si 3 - 5x < 0, x > 3/5, alors
l'inéquation (4) s'ecrit:
(2x - 7)(3 - 5 x) ≥ (17 x + 5)
ou
0 ≥ 5x2 - 12 x + 13
Le trinôme 5x2 - 12 x + 13 n'a pas de racines.
Il est toujous postif puisque le signe du coefficient
de x2 qui est 5 est positif. L'ensemble
des solutions est donc l'ensemble vide. Avec
la contrainte x > 3/5, l'ensemble des
solutions reste toujours doc l'ensemble vide.
S2b = {} = Φ.
Ainsi, l'ensemble des solutions de l'inéquation (4)
est S2 = S1b ∪ S2b = ]- ∞, 0.6[ ∪ {} =
]- ∞, 0.6[.
S2 = ]- ∞, 0.6[
L'ensembe des solutions de l'equation donnée est
S = S1 ∩ S2 = [0.29, 0.6[ ∪ [5.51, + ∞[ ∩ ]- ∞, 0.6[
= [0.29, 0.6[
Compte tenu de la contrainte de départ, l'ensemble
des solutions doit être contenu dans
S0 = [- 5/17, 3/5[ = [- 0.294, 0.6[
Ce qui est bien le cas.
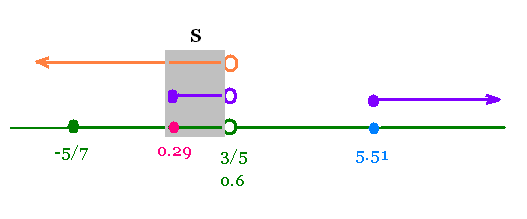
Ainsi, l'ensemble des solution de
l'inéquation donnée est:
S = [0.29, 0.6[
|
|