Mathématiques 2: Fonction réciproque
1. Définition
Une fonction f associe à chaque
variable indépendante x une variable dépendante y.
On a:
f: x → y = f(x)
La fonction réciproque fr fait l'inverse. Elle associe à
chaque valeur y une valeur x. Le codomaine de f devient le domaine de fr.
On a:
x = fr(y) ← y : fr
r signifie:réciproque. On usitilise aussi la notation f-1 pour
la fonction réciproque.
Bien entendu r et -1 ne sont pas des exposants.
2. Examples
2.1. Example 1
La fontion f associe à chaque x la valeur y:
y = 2 x - 1
On résoud l'équation et l'on obtient:
2x = y + 2
Donc x = (y + 1)/2
La fonction qui à y on associe x est la fonction
réciproque ou la fonction inverse fr de la fonction f .
2.2. Example 2
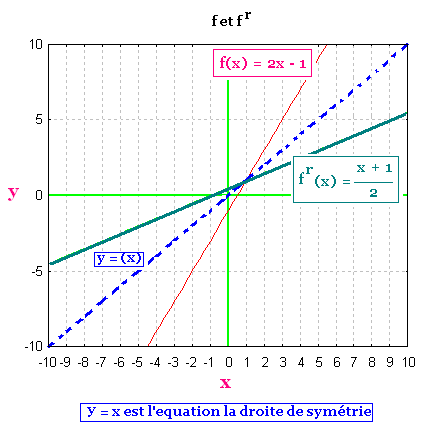
Voici les graphes de la fonction f et celui de sa
fonction réciproque fr.
La droite de la fonction de symetrie y = x a été aussi représentée.
2.3 Example 3
Toutes les fonctions n'ont pas nécessairement des
fonctions réciproques. Par exemple:
La fonction carré transforme x en son carré:
y = f(x) = x2
f : x → y = f(x) = x2
Par exemple f(+ 2) = (+2)2 = 4 . Mais nous avons aussi
f(- 2) = (- 2)2 = 4
La réciproque de la fonction carré est racine carrée:
x ← y = x2
Mais pour une valeur de y, comme 4, nous avons deux valeurs
de x comme + 2 et - 2.
Donc cette réciproque n'est pas une fonction.
Pour que cette réciproque soit une fonction, on omet
l'ensemble des valeurs négatives. Ainsi la réciproque
devient bien une fonction. Le codomaine de cette fonction
réciproque n'est pas R, mais juste R+:
La racine carrée (√) est une fonction dont
le domaine est R+ et le codomaine est R+.
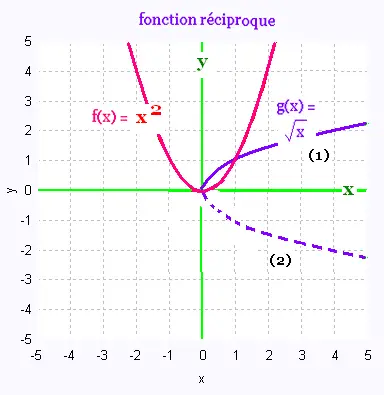
On supprime la partie (2) pour que la réciproque devienne
une fonction. Ainsi on obtient la fonction racine carrée
de base f(x) = √x.
3. Exercices
3.1. Exercice 1
Quelle est la fonction réciproque de la fonction f
telle que:
f(x) = y = (x + 1)/x
Réponse:
x = 1/(y - 1)
3.2. Exercice 2
a)
Quelle est la fonction réciproque de la
fonction f telle que:
f(x) = y = x + 3
dom f = [0, 6[
b)
Représenter sur un plan cartésien la courbe
de la fonction f.
c)
Représenter sur le même plan la courbe
de la fonction réciproque fr
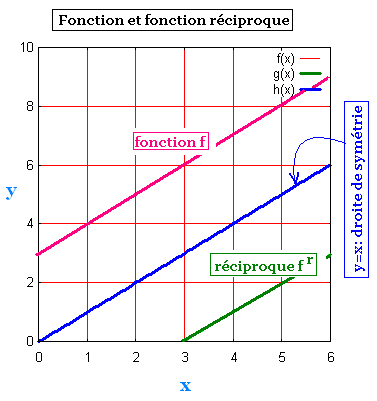
d)
Pour vérifier la symétrie de la fonction f par rapport à
sa fonction réciproque fr, représenter sur le même
plan la courbe de la fonction y = x.
Réponse:
|