Mathématiques 2: Fonctions
1. Le mot clé
Une fonction est une relation entre deux ensembles.
Le premier ensemble est constitué de variables de la fonction.
Le deuxième ensemble est constitué des images de la variable.
La fonction possède la propriété que chaque variable possède
exactement une et une seule image.
La fonction f transforme la variable indépendente
x en la variable dépendente y. On ecrit:
y = f(x)
x est la variable, y est son image.
Dans le plan cartésien, x est
l'abscisse, y est l'ordonné du
point P(x,y).
2. Exemple
On relève les températures chaque jour
exactement à midi durant une semaine à Montréal.
On place les résultats trouvés dans le tableau
des valeurs suivant:
| la variable | son image |
| jour de la semaine | température en °C |
| Dimanche | 0 |
| Lundi | - 3 |
| Mardi | - 5 |
| Mercredi | + 2 |
| Jeudi | +4 |
| Vendredi | +4 |
| Samedi | + 1 |
Il est clair que pour chaque jour, il ne
correspond qu'une seule valeur de
température prise à midi.
Ainsi la relation entre les jours et les températures
est bien une fonction.
Si on change le jour, on change la température, et
l'inverse n'est pas possible.
Le chagement de jours IMPLIQUE le changemenet de température.
Le jour = variable indépendante
La température = variable dépendante
Graphique de la fonction
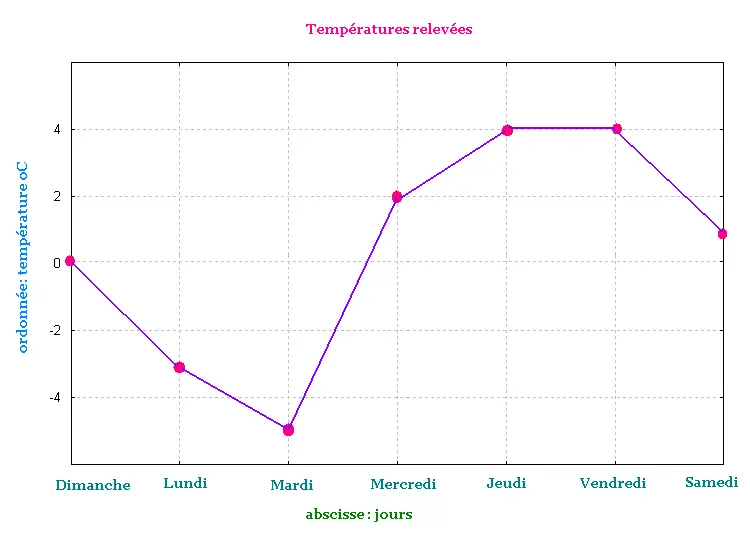
3. Autres exemples
3.1. Distance au centre du carré à
partir d'un point sur le carré
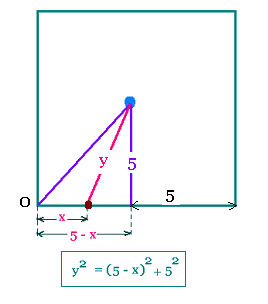
On veut représenter la distance au centre du carré en
fonction da la distance parcourue sur ce carré.
À la distance x à partir de O, on a
y2=(5-x)2+52
On construit un tableau de valeurs:
| la variable x | son image y |
distance parcourue
sur le carré (cm) | distance au
centre du carré (cm) |
| 0 | 5√2 = 7.07 |
| 1 | 6.4 |
| 2 | 5.8 |
| 3 | 5.4 |
| 4 | 5.1 |
| 5 | 5 |
Et on complète par symétrie de 5 à 10; puis
de 10 à 20, puis de 20 à 30 et ensuite
de 30 à 40. On obtient le graphique suivant:
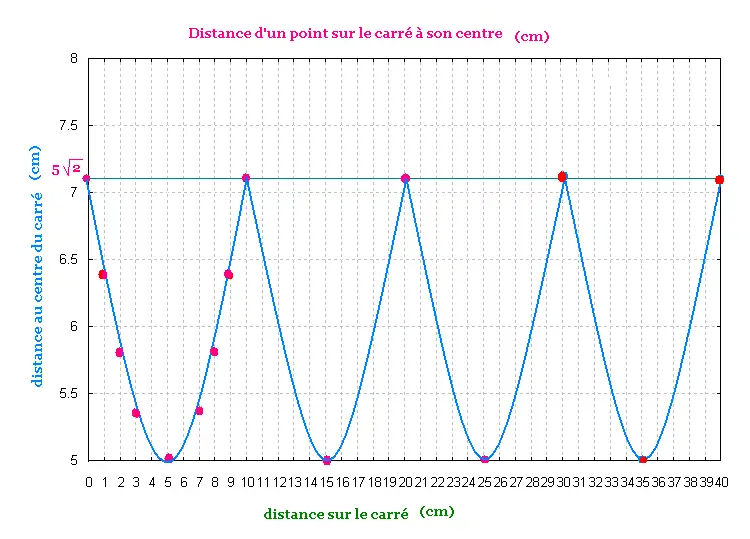
3.2. Hauteur d'une colonne de liquide
On remplit le contenant suivant:
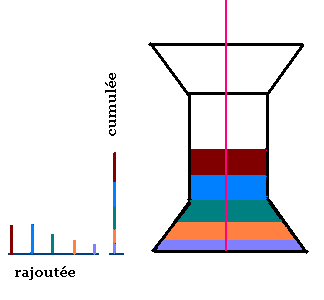
À chaque seconde, on ajoute un même volume
V de liquide dans le contenant.
On s'interesse à la hauteur de la colonne
de liquide obtenue.
La hauteur de la colonne
de liquide est une fonction du volume de liquide
rajouté.
On peut faire deux graphiques:
a)
Graphique de la colonne de liquide cumulé;
c'est à dire la hauteur obtenue en rajoutant à chaque fois
le volume V de liquide au volume déjà présent. On obtient:
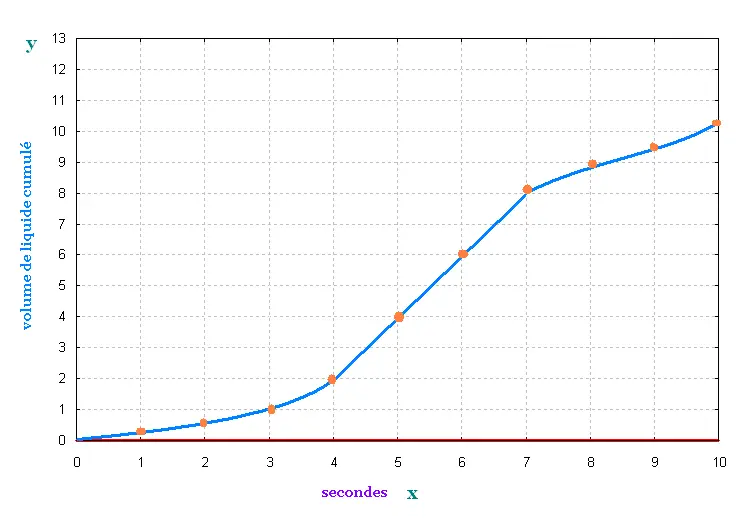
la variable x est le temps en secondes: chaque seconde,
on rajoute un même volume V de liquide.
La variable y est la hauteur de la colonne de liquide
cumulé à chaque fois.
y = f(x)
b)
Graphique de la colonne de liquide rajoutée à chaque
seconde:
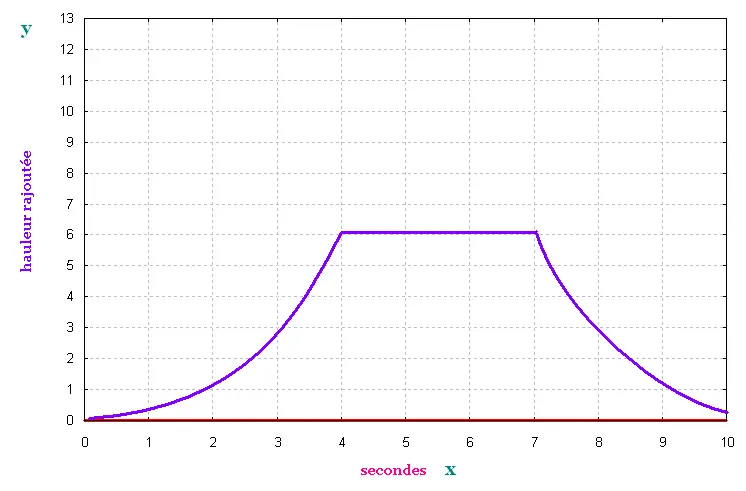
la variable x est le temps en secondes: chaque seconde,
on rajoute un même volume V de liquide.
La variable y est la hauteur de la colonne de liquide
rajoutée à chaque fois.
y = f(x)
Le contenant est symétrique, le graphique aussi.
|

