Mathématiques 2: Propriétés graphiques d'une fonction

1. Domaine et codomaine d'une fonction:

Le domaine ou le domaine de définition d'une fonction est l'ensemble de toutes les valeurs que prend la variable indépendante de la fonction.
C’est aussi l’ensemble des valeurs qui ont une image par la fonction. Le domaine d’une fonction f est noté dom f.

Le codomaine ou image est l'ensemble de toutes les valeurs que prend la variable dépendante de la fonction.
C’est l’ensemble des images des éléments du domaine. Le codomaine d’une fonction f est noté codom f ou ima f.

Example:

Je dois remplir une bassine d'eau. La bassine ne peut prendre que 20 litres d'eau. À chaque heure, je dois verser 4 litres d'eau. Ainsi, au bout de 5 heures, j'aurais rempli toute la bassine.

La variable indépendente x est l'heure. Sa variable dépendente y correspondante et le volume total(cumulé) d'eau versé dans la bassine.

y = f(x)

f est la fonction de verser x litres d'eau pour obtenier un volume cumulé y d'eau correspondant.

Pour chaque x, on a au plus un y, voir un seul y; alors f est une fonction.

On ecrit donc:
f(x) = 4 x

l'ensembre des heures de 0 à 5 [0,5] est le domaine de la fonction f. L'ensemble des litres d'eau obtenus de 0 à 20 [0,20] est le codomaine de la fonction f.

On represente graphiquement cette fonction sur un plan cartésien et on obtient le graphique suivant:

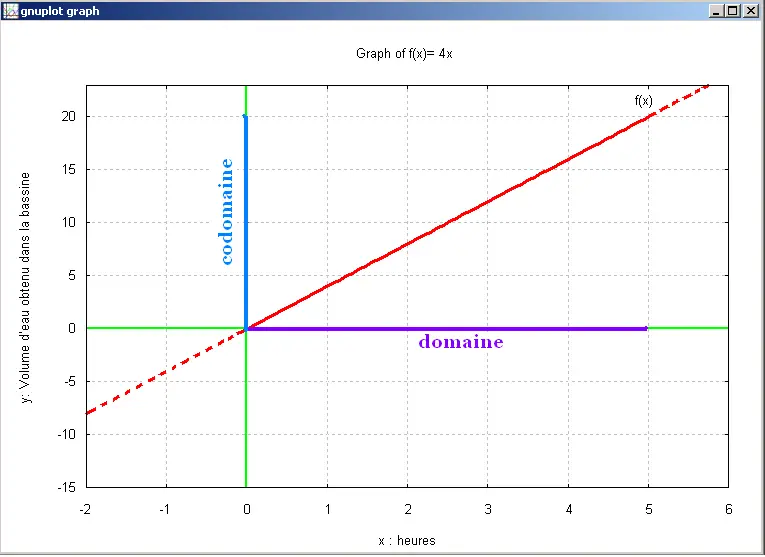
2. Variation et signe d'une fonction:

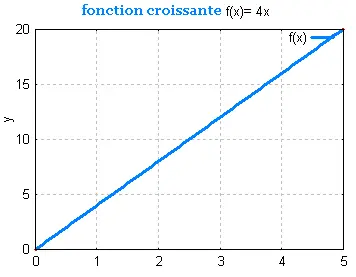
Une fonction est croissante si la variable y varie dans le même sens que la variable x. C'est à dire: au fur et à mesure que x croit y croit aussi.

La courbe de la fonction monte.



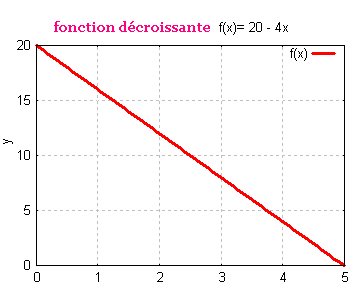
Une fonction est décroissante si la variable y varie dans le sens contraire de la variable x. C'est à dire: au fur et à mesure que x croit y décroit.

La courbe de la fonction descend.



Une fonction est constante si elle est n'est pas croissante et elle n'est pas décroissante.



Une fonction est positive si y est positif pour toute valeur de x. Son codomaine ne comporte que des nombres positifs.



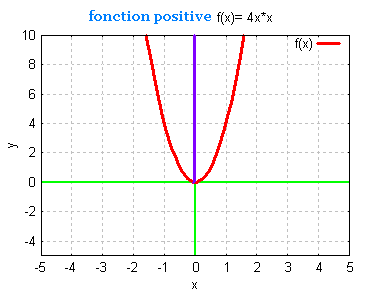
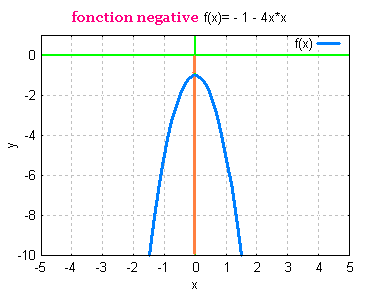
Une fonction est négative si y est négatif pour toute valeur de x. Son codomaine ne comporte que des nombres négatifs.

3. Extremums d'une fonction:

Un extremum (pluriel : extremums ou extrema) est un maximum ou un minimum.



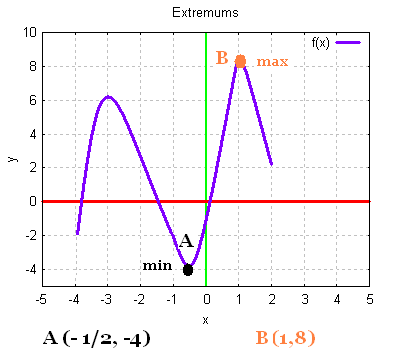
Le minimum d'ne fonction f est le point qui correspnd à la plus petite des valeurs de f(x).

Le maximum d'une fonction f est le point qui correspnd à la plus grande des valeurs de f(x).

Le point A est un minimum. Le point B est un maximum.

4. Les zéro d'une fonction:

Le zéro d'une fonction est la valeur de x qui annule cette fonction. C'est à dire les valeurs de x pour lequelles y = 0.

Une fonction possède un ou plusieurs zéros. Les zéros d'une fonction sont les points où la courbe de la fonction coupe l'axe des abscisses x.



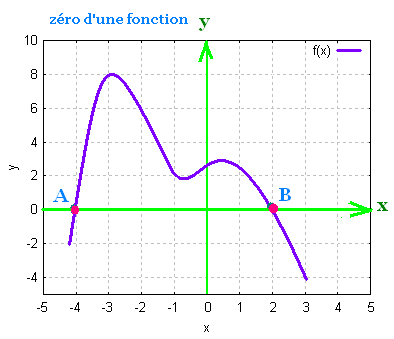
Les zéro de cette fonction sont x = - 4 et x = + 2