Mathématiques 2: Fonctions exponetielles
1. f(x) = - 3 log3((x - 2)/2) + 1
Domain :
(x - 1)/2 > 0 → x > 1
f(x) = 0 si log3((x - 2)/2) = 1/2
c'est à dire (x - 2)/2 = 31/2
x = 2 x 31/2 + 2
Utiliser la formule de changement de base:
loga(x) = logb(x)/logb(a)
donc
loga (x) = loge (x)/loge(a)
ou
loga (x) = ln(x)/ln(a)
f(x) = - 3 [ln((x - 2)/2)]/ln(3) + 1
Graphe:
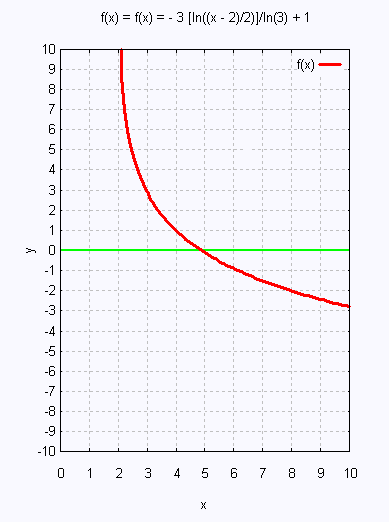
2. log2(x) = 5
log2(x) = 5
x = 25 = 32
3. 3 ln(3 x - 2) - 2 = - 7
3 ln(3 x - 2) = - 5
ln(3 x - 2) = - 5/3
3 x - 2 = e- 5/3
x = [e- 5/3 + 2]/3
4. log6(2x - 1) + 2 log6 -
log6(3x - 2) = 3
log6(2x - 1) + log62 -
log6(3x - 2) = 3
log6[(2x - 1) . 62 . (3x - 2)] = 3
[(2x - 1) . 62 . (3x - 2)] = 63
(2x - 1) . (3x - 2) = 6
6 x2 - 7 x + 2 = 6
6 x2 - 7 x - 4 = 0
Δ = (- 7)2 - 4 (6)(- 4) = 49 + 96 = 145
Deux solutions:
x1 = (7 - 12.04)/12 = - 0.42
x2 = (7 + 12.04)/12 = 1.59
5. 4log4(2x) = x + 1
4log4(2x) = x + 1
(2x) = x + 1
x = 1
6. log5(2x - 5) - 4 ≥ 3
log5(2x - 5) ≥ 7
(2x - 5) ≥ 57
x≥ [57 + 5]/2
7. 3 log5(2x3/k)
x = 3.4
k = 1.2
y = 3 log5(2x3/k) =
3 [log5(2x3) - log5(k)] =
3 [log5(2) + 3log5(x))
- log5(k)] =
3 log5(2) +9 log5(x) - 3 log5(k)
3 log5(2) + 9 (3.4) - 3 (1.2)
log5(2) = log10(2)/log10(5) =
= ln(2)/ln(5)
y = 3 ln(2)/ln(5) + 9 (3.4) - 3 (1.2) =
3 x 0.69 /1.61 + 9 (3.4) - 3 (1.2) = 1.29 + 30.6 - 3.6 =
28.29
y = 28.29
8. logx((5kx)3)
x = 3.4
k = 1.2
y = logx((5kx)3) =
3 logx(5kx) = 3 [logx(5) + logx(k) + logx(x)]
=
3 [logx(5) + logx(k) + 1]
logx(X) = ln(X)/ln(x)
y = 3 [log3.4(5) + log3.4(1.2) + 1] =
3 [ln(5)/ln(3.4) + ln(1.2)/ln(3.4) + 1] =
3 [1.61/1.22) + 0.18/1.22 + 1] =
3 [1.32 + 0.15 + 1] = 7.41
y = 7.41
8. f(x) = 4 ln(5x - 10) + 1
f(x) = 4 ln(5x - 10) + 1
y = 4 ln(5x - 10) + 1
y - 1 = 4 ln(5x - 10)
(y - 1)/4 = ln(5x - 10)
e(y - 1)/4 = eln(5x - 10) = 5x - 10
e(y - 1)/4 = 5x - 10
e(y - 1)/4 + 10 = 5x
x = [e(y - 1)/4 + 10]/5
La fonction réciproque de f(x) est g(x) telle que:
g(x) = [e(x - 1)/4 + 10]/5
|