Mathématiques:
Géométrie
Définition d'un angle
Mesure d'un angle

les angles

1. Définition d'un angle

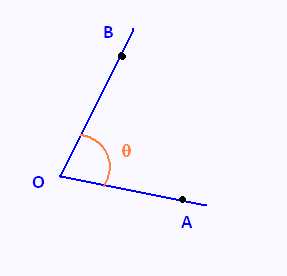
Un angle est une figure géométrique où une portion d'espace représentée par deux demi-droites de même origine.

$\widehat{AOB}$ est un angle.

$\widehat{AOB} = \widehat{BOA}$


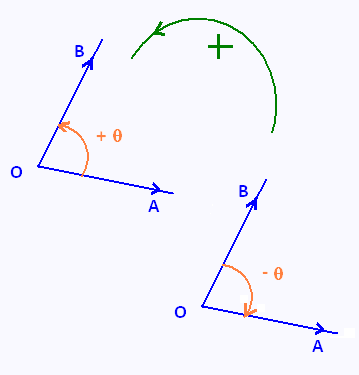
En Analyse vectorielle, un plan est orienté. Les angles dans ce plan sont aussi orientés. Dans ce cas un même angle peut être aussi bien positif que négatif, selon le sens dans lequel on « tourne » du premier vecteur au second.

Par convention, on oriente le plan dans le sens « trigonométrique », c'est-à-dire dans le sens inverse des aiguilles d'une montre (ou « sens anti-horaire »).

Si l'on considère deux demi-droites ou vecteurs, alors l'ordre dans lequel on cite les demi-droites ou les vecteurs définit le sens de l'angle, donc son signe ; ainsi :

$\widehat{AOB} = - \widehat{BOA}$

$\widehat{AOB} = (\widehat{\vec{OA},\vec{OB}})$ ,      $\widehat{BOA} = (\widehat{\vec{OB},\vec{OA}})$

2. Mesure d'un angle

On confond fréquemment angle et mesure de l'angle . D'une façon correcte, si un angle mesure 55^o, on ecrit:

mes ($\widehat{AOB}$) = 55^o

On mesure un angle en degré ou en radian. En astronomie, on utilise aussi des minutes d’arc et des secondes d'arc.

Un degré est subdivisé en 60 minutes d’arc (symbole: '), elles-mêmes divisées en 60 secondes d’arc (symbole: ").

Un degré = 60 minutes d’arc : 1^o = 60'.
Une minute = 60 secondes d’arc: 1' = 60"

La circonférence d'un cercle de rayon r, c'est à dire son périmètre mesure 2π r unités. Celle d'un cercle trigonométrique est égale à 2π unités. Ves unités sont le radians ou rad .

Ces 2π radians sont équivalentes à 360^o
2π rad ≡ 360^o . Donc 1 rad ≡ 360/2π = 57.295^o
1 rad 57.295^o


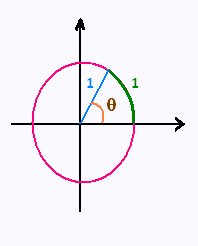
Un angle au centre qui sous-tend un arc de longueur égale au rayon mesure 1 rad = 57.295^o