Mathématiques: Algèbre
La fonction logarithmique
Bürgi, les premières approches
Neper et le logarithme
Henry Briggs , le log

Bürgi, les premières approches

En Europe, du 15e au 16e siècle, l'industrie, la navigation, l'astronomie et le commerce se développaient et nécessitaient alors plus d'études et de professionnalisme.

L'exemple des opérations banques qui incluaient le calcul de l'intérêt composé, ont motivé Joost Bürgi un mathématicien, astronome et horloger suisse (1552-1632), travaillant dans la précision des instruments pour le morché; à créer une table qui est plus rapide à utiliser que les tables existantes de calcul de l'intérêt composé.

Pour un taux d'intérêt p donné, Bürgi construit les termes de la progression géométrique (1 + p/100)ⁿ, où n = 0,1,2, ..., les termes correspondants de la progression arithmétique sont 0, 10, 20, ..., 10n.

Ainsi, pour le produit de deux termes quelconques de la séquence géométrique d'origine, il y a un terme correspondant de la progression arithmétique qui est obtenu en additionnant les termes correspondants aux deux termes multipliés. Burgi songait déjà à remplacer des multiplications ou divisions par des additions ou de soustarction.

Dans l'actuelle notation on a logarithm-burgui (1 + p/100)ⁿ = 10n.

Jost Bürgi travaillait aux côtés de Kepler à Prague. Il élabore des tables trigonométriques et une table dite d' antilogarithmes (exponentielles) qui sera publiée en 1620.

Bien qu'il ait terminé sa table en 1611, Bürgi l'a publiée seulement neuf ans plus tard. Mais le mathématicien écossais John Napier publia ses ses logarithmes en 1614.

Voici la table de Bürgi. Elle s'étend pour les nombres noirs de 10⁸ à 10⁹:


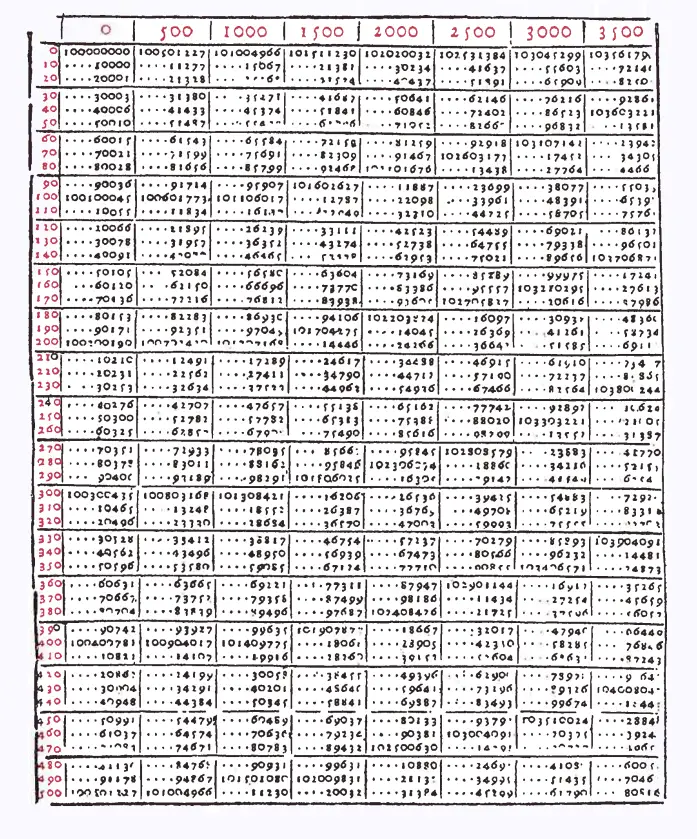
Jost Bürgi a conçu cette table de correspondance entre une suite géométrique de premier terme 10⁸ et de raison 1.0001 (nombres noirs arrondis à l'unité) et une suite arithmétique de premier terme 0 et de raison 10 (nombres rouges).

À une multiplication des nombres noirs suivie d'une division par 10⁸, correspond alors une addition dans les nombres rouges.

Pour calculer le produit de deux nombres (noirs), il suffit de rechercher leur correspondant rouge, d'en faire la somme (rouge), d'en rechercher le correspondant noir et de le multiplier par 10⁸.

En termes actuels, le nombre rouge y est lié au nombre noir x par la relation:

y = 10 log_1.0001(x/10⁸)

Bürgi publie tardivement en 1620 soit 6 ans après la publication de Neper et les premières éditions sont privées de l'introduction qui aurait permis d'en comprendre le fonctionnement. Ce sont ces deux faits qui expliquent le peu de succès rencontré par les tables de Bürgi.