Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre & Géométrie
Les fonctions trigonométriques
Les équations trigonométriques
1. L'équation trigonométrique en sinus
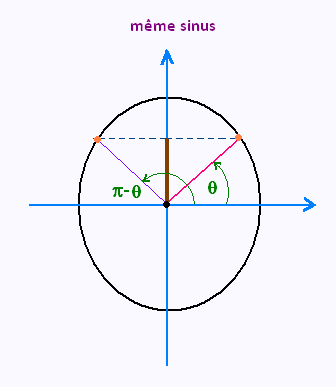
L'équation :
sin x = a
a pour solution x = arcsin (a) = sin-1(a) . On le fait
avec une calculette.
• On n'oblie pas de faire des tours ... Donc
x = Arcsin (a) + 2kπ , k est un entier relatif .
• Mais ce n'est pas fini, π - x est aussi solution
avec des tours également. Donc
x = π - Arcsin (a) + 2kπ , k est un entier relatif .
Finalement,
Les solutions de l'équation
sin x = a sont
x = Arcsin (a) + 2 k π et
x = π - Arcsin (a) + 2 k π
k ℤ ℤ
2. L'équation trigonométrique en cosinus
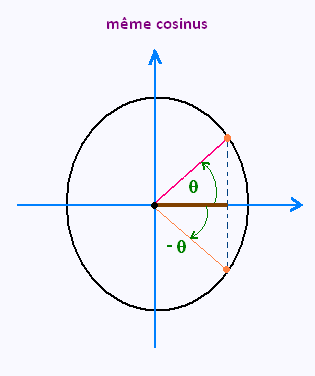
L'équation :
cos x = a
a pour solution x = Arccos(a) = cos-1(a) . On le fait
avec une calculette.
• On n'oblie pas de faire des tours ... Donc
x = Arccos(a) + 2kπ , k est un entier relatif .
• Mais ce n'est pas fini, - x est aussi solution
avec des tours également. Donc
x = - Arcsin (a) + 2kπ , k est un entier relatif .
Finalement,
Les solutions de l'équation
cos x = a sont
x = Arccos (a) + 2 k π et
x = - Arccos (a) + 2 k π
k ℤ ℤ
3. L'équation trigonométrique en tangente
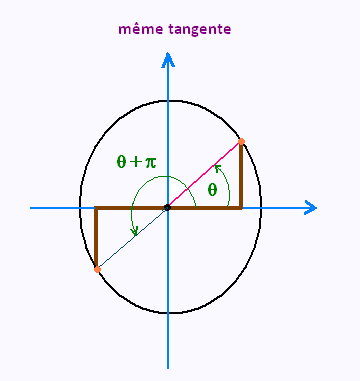
L'équation :
tan x = a
a pour solution x = Arctan(a) = tan-1(a) . On le fait
avec une calculette.
• On n'oblie pas de faire des tours ... Donc
x = Arctan(a) + 2kπ , k est un entier relatif .
• Mais ce n'est pas fini, π + x est aussi solution
avec des tours également. Donc
x = π + arctan (a) + 2kπ , k est un entier relatif .
Finalement,
Les solutions de l'équation
tan x = a sont
x = Arctan(a) + 2 k π et
x = π + Arctan (a) + 2 k π
k ℤ ℤ
Ce qui est équivalent à:
x = Arctan(a) + k π
k ℤ ℤ
4. Résumé

|
|