Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre
La fonction exponentielle
Équations et Inéquations simples
1. La méthode algébrique
• Transformer les deux membres de l'équation de telle sorte
qu'ils auront ume même base,
• Résoudre l'équation ou l'inéquation aux exposants.
2. Exemple : cas d'une équation
On considère l'équation suivante:
3(1/5)x - 1 - 375 = 0
(1/5)x - 1 = 375/3 = 125
51 - x = 53
1 - x = 3
d'où:
x = - 2
L'equation est dite simple puisque le deuxième membre de
l'équation, ne comportant pas la variable x, est facilement
transformable en la base du membre de droite de
l'équation. C'est à dire 125 = 53.
Lorsque ce n'est pas le cas, il faut passer par le logarithme,
fonction inverse de la fonction exponetielle.
3. Méthode graphique
• On trace le gpagique des expressions des deux membres
de l'équation, ou de l'inéquation,
• On compare les valeurs des ordonnées, et
• On en déduit les valeurs des x correspondants.
Exemple : cas d'une inéquation:
On considère l'inéquation suivante:
4(3)2x + 1 - 28 ≤ 0
4(3)2x + 1 ≤ 28
(3)2x + 1 ≤ 7
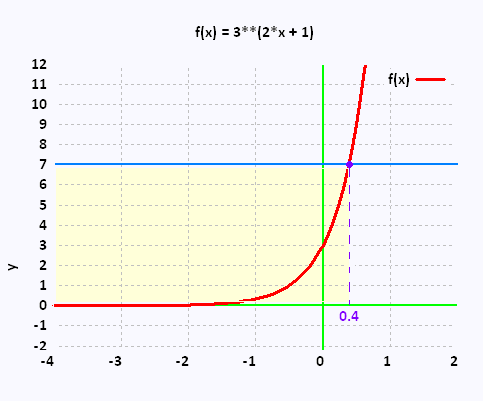
Graphiquement, le point d'intersection de la courbe
exponentielle et la droite horizontale x = 7 est x ≈ 4
L'ensemble solution est donc:
S = ]- ∞, 0.4[
|
|