Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre
La fonction logarithmique
Zéro d'une fonction logarithmique
L'ordonnée à l'origine d'une fonction logarithmique
Analyse d'une fonction logarithmique
1. Zéro d'une fonction logarithmique
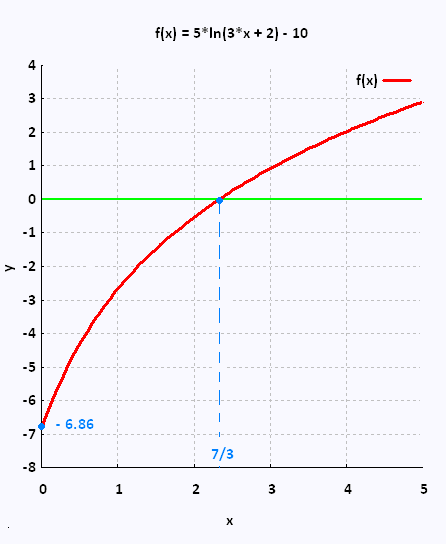
Soit la fonction logarithmique suivante:
f(x) = 5 log3(3 x + 2) - 10
• Il faut tout d'abord évaluer la contrainte: 3 x + 2 > 0.
Ce qui donne:
x > -2/3
• On cherche le zéro de la fonction f:
f(x) = 0 donne:
log3(3 x + 2) = 2. D'où:
3 x + 2 = 32 = 9
x = 7/3
Cette solution respecte la contrainte
x > -2/3
Ainsi
x = 7/3 est le zéro de la fonction.
Graphiquement, nous avons:
2. L'ordonnée à l'origine d'une fonction logarithmique
Soit la fonction logarithmique suivante:
f(x) = 5 log3(3 x + 2) - 10
L'ordonnée à l'origine de cette fonction logarithmique s'obtient par
l'évaluation de f(0).
On a donc:
f(0) = 5 log3(3 (0) + 2) - 10 = 5 log3(2) - 10 = - 8.86
Ainsi
y = - 6.86 est l'ordonnée à l'origine de la fonction.
3. Exemple d'analyse d'une fonction logarithmique
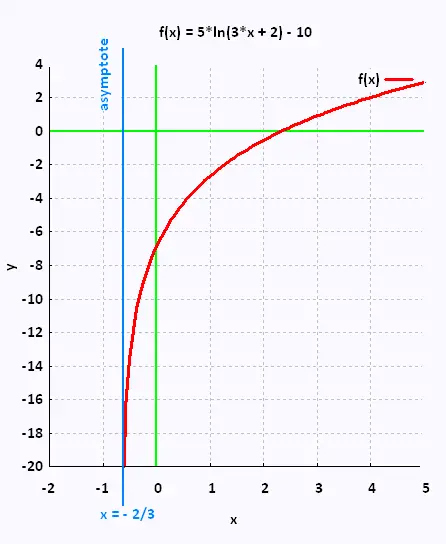
Soit la fonction logarithmique suivante:
f(x) = 5 log3(3 x + 2) - 10
• Contrainte: 3 x + 2 > 0.
Ce qui donne:
x > -2/3
• Les zéros de la fonction f:
f(x) = 0 donne:
log3(3 x + 2) = 2. D'où:
3 x + 2 = 32 = 9. Donc
x = 7/3
Cette solution respecte la contrainte
x > -2/3 .
Ainsi
x = 7/3 est le zéro de la fonction.
• L'ordonnée à l'origine de cette fonction logarithmique s'obtient par
l'évaluation de f(0).
On a donc:
f(0) = 5 log3(3 (0) + 2) - 10 = 5 log3(2) - 10 = - 8.86.
Ainsi
y = - 6.86 est l'ordonnée à l'origine de la fonction.
• L'asymptote de la fonction logarithmique est une asymptote
verticale. Elle s'obtient par une valeur de x qui annule la variable
du log:
Dans la fonction f(x) = 5 log3(3 x + 2) - 10, la
valeur de x qui annule la variable du log est telle que 3 x + 2 = 0.
c'est à dire x = - 2/3
L'asymptote de la fonction est x = - 2/3.
• Graphique de la fonction:
Resumé:
Domf = ]-2/3, +∞[
Imf = R
zéro: x = 7/3
ordonnée: y = - 6.86
Extrema: aucun
croissance : dans R
decroissance: aucune
f(x) ≥ 0 dans [7/3, +∞[
f(x) < 0 dans ]-2/3, 7/3[
|
|