Mathématiques 2: Fonction rationnelle
Inéquations avec la fonction rationnelle

1. Inéquations avec la fonction rationnelle

Il suffit de résoudre une inéquation de proportions en excluant, bien sûr, le pôle de la fonction rationnelle., c'est à dire les racines du polynôme ou les valeurs de x qui annulent le dénominateur.

L'inégalité impose alors la propriété de changer l'ordre lorsqu'on multiplie ou divise les deux mmembres de l'inégalité par un nombre négatif. C'est à dire:

Si $\Large\bf\color{green}{ \frac {a x + b}{c x + d} \le m }$ , alors

• si c x + d > 0 alors $\bf\color{brown}{ a x + b \le m (c x + d) }$

• si c x + d < 0 alors $\bf\color{brown}{ a x + b \ge m (c x + d) }$

On peut aussi transposer le membre de droite à gauche et traiter directement l'ordre de la fonction rationnelle. C'est à dire:

$\Large\bf\color{green}{ \frac {a x + b}{c x + d} - m \le 0 }$

Donc

$\Large\bf\color{blue}{ \frac {(a x + b) - m(c x + d)}{c x + d} \le 0 }$

Géméralement,

Si $\Large\bf\color{red}{ \frac {a x + b}{c x + d} \le \frac {m x + n}{p x + q} }$

On transpose le fraction de droite, on réduit au même dénominateur et on résoud l'inéquation avec un tableau de signes.

$\large\bf\color{green}{ \frac {a x + b}{c x + d} - \frac {m x + n}{p x + q} \le 0 }$

$\Large\bf\color{tomato}{ \frac {(a x + b)(p x + q) - (m x + n)(c x + d)}{(c x + d)(p x + q)} \le 0 }$

L'ordre de l'inégalité choisie et ≤. Les mêmes opérations sont valides pour les autres types d'ordre: >, ≥, ou <.

2. Exemple:

$\Large\bf\color{green}{ \frac {3 x + 12}{5 x + 2} \ge 3 }$

D'abord, x ≠ - 2/5: Dom = R \ {- 2/5} .

• x > - 2/5 : 3 x + 12 ≥ 3(5x + 2)

3 x + 12 ≥ 15x + 6 → 6 ≥ 12x → x ≤ 1/2

S1 = ] - 2/5, + ∞ [ ∩ ] - ∞, 1/2] = ] -2/5, 1/2]

• x < - 2/5 : 3 x + 12 ≤ 3(5x + 2)

3 x + 12 ≤ 15x + 6 → 6 ≤ 12x → x ≥ 1/2

S2 = ] - ∞, -2/5 [ ∩ [1/2, + ∞[ = { }



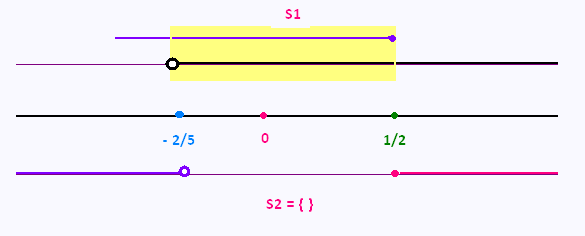
S1 = ] -2/5, 1/2] , S2 = {} , donc
S1 ∪ S2 = S2 . L'ensemble solution est donc :
S = ] -2/5, 1/2]

3. Méthode graphique :

Soit à resoudre l'équation:

$\Large\bf\color{green}{ \frac {3 x + 12}{5 x + 2} \ge 3 }$

On trace l'horizontale y = 3 et on cherche le point d'intersection de cette horizontale avec la courbe de la fonction rationnelle, qui est x = 1/2.

Seuls les points allant de -2/5 à 1/2 répondent à la question:

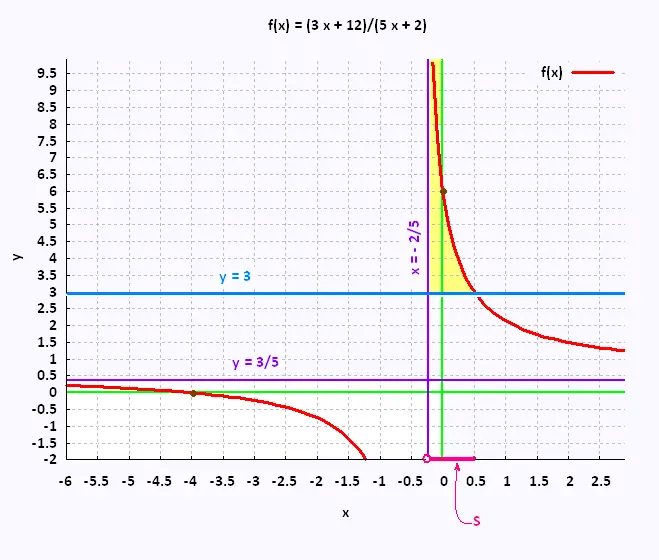
3. Méthode de tableau de signes:

Soit à résoudre l'équation:

$\Large\bf\color{green}{ \frac {3 x + 12}{5 x + 2} \ge 3 }$

$\Large\bf\color{indigo}{ \frac {3 x + 12}{5 x + 2} - 3 \ge 0 \\ \frac {3 x + 12 - 15 x - 6 }{5 x + 2} \ge 0 }$

$\Large\bf\color{red}{ P(x) = \frac { - 12 x + 6 }{5 x + 2} \ge 0 }$



Seuls les points allant de -2/5 = - 0.5 à 1/2 = 0.5 répondent à la question: