Mathématiques:
Algèbre
Les fonctions trigonométriques
Les fonctions sinusoidales

1. Définition d'une fonction sinusoidale

Une fonction sinusoidale est une fonction décrite par la fonction sinus, c'est à dire par la dépendence d'un angle et de son sinus trigonométrique.

Voici le graphe de cette fonction sinus:



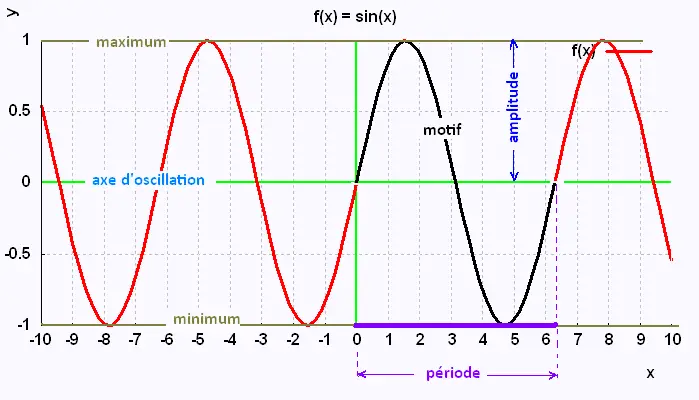
Les fonctions sinusoidales sont des fonctions périodiques, c'est à dire qu'elles décrivent des situations qui se répètent régulièrement.

Dans le graphique d'une fonction sinusoidale, un motif ou cycle se répète indéfiniment dans le tracé.

La période est la longueur de l'intervalle où est défini le motif. Ici elle vaut 6.28 = 2π.

L'amplitude est la moitié de la longueur de l'intervalle entre le maximum et le minimum. Ici elle vaut [1 - (- 1) ]/2 = 1.

L'axe des oscillations est la droite horizontale située au milieu du tracé entre le maximum et le minimum.

2. Définition générale d'une fonction sinusoidale

On sait que lorsque deux angles sont complémentaires, le sinus de l'un est égal au cosinus de l'autre et vise versa.

C'est à dire si a + b = π/2 , alors
sin(a) = cos(b) = cos (π/2 - a) et
cos(a) = sin(b) = sin (π/2 - a) .

De ce fait,

les fonctions f(x) = sin(x) et f(x) = cos (π/2 - x) sont équivalentes.

les fonctions g(x) = cos(x) et g(x) = sin (π/2 - x) sont équivalentes.

Mieu encore, on sait que:

la fonction sinus est impaire f(- x) = - f(x) et
la fonction cosinus est paire f(- x) = f(x) , donc

cos (π/2 - x) = cos (- (x - π/2)) = cos (x - π/2), et
sin (π/2 - x) = sin (- (x - π/2)) = - sin (x - π/2)

Ainsi:

les fonctions f(x) = sin(x) et
f(x) = cos (x - π/2) sont équivalentes.

les fonctions g(x) = cos(x) et
g(x) = - sin (x - π/2) sont équivalentes.




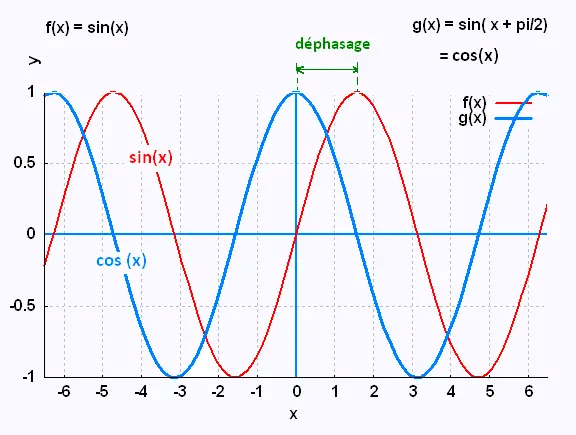
Une fonction sinusoidale peut donc être aussi bien décrite par un sinus d'un cosinus.

La forme canonique d'une fonction sinusoidale est la suivante:

                    f(x) = a sin [b(x - h)] + k

Les paramètres a, b, h et k sont des nombres réels.