Mathématiques:
Algèbre & Géométrie
Les fonctions trigonométriques
La fonction sinusoidale
les paramètres et le graphique

1. Les paramètres et le graphique

L'équation canonique d'une fonction sinusoidale s'ecrit:

       f(x) = a sin [b(x - h)] + k , ou

         f(x) = a cos[b(x - h)] + k


• L'équation de l'axe d'oscillation est y = k

• Le maximum de la fonction est |a| + k

• Le minimum de la fonction est - |a| + k

• La période de la fonction est P = 2π/|b|

• La fonction sinus f(x) est croissante au point (h,k) si a . b > 0.
Elle est décroissante en ce point si a . b. < 0.

• La fonction cosinus g(x) est croissante au point (h,k + a) si a > 0.
Elle est décroissante en ce point si a < 0.

2. Exemple

Soit la fonction sinusoidale suivante:

f(x) = 3 sin [(- 2/3)(x - π/2)] + 1

• L'équation de l'axe d'oscillation est y = 1

• Le maximum de la fonction est 4

• Le minimum de la fonction est - 2

• La période de la fonction est P = 2π/|(-2/3)| = 3π

• La fonction est décroissante au point (π/2, 1)
puisque a . b = 3 (-2/3) = - 2 est < 0 .

Voici le graphique de cette fonction :



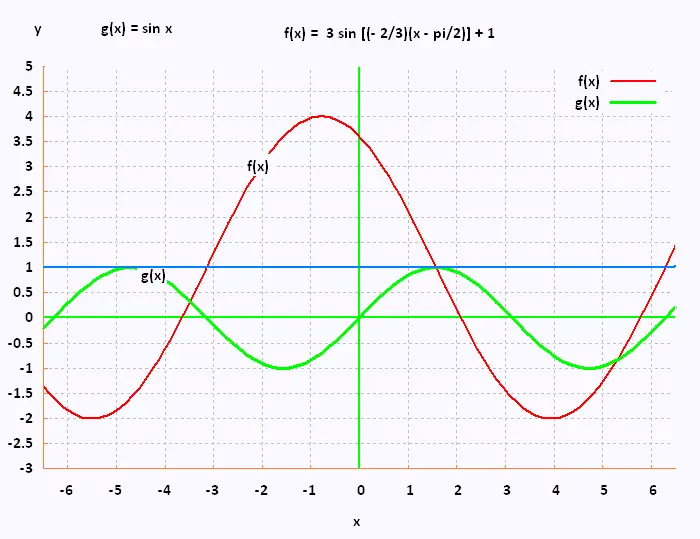
Tout se passe cpmme si à partir de la fonction sinusoidale de base g(x) = sinx, on effectue:

• Une translation horizontale du tracé de x = h = π/2,
appelé aussi déphasage,

• Une translation horizontale du tracé de y = k = 1,

• L'axe d'oscillation passe de 0 à y = k = 1,

• On dilate le tracé grace à la période qui passe
de P = 2π à P = 2π/|b| = 2π/|(-2/3)| = 3π,

• On dilate l'amplitude de 1 à |a| + 1 = 3 + 1 = 4