Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre & Géométrie
Les fonctions trigonométriques
La fonction tangente
Résolution d'équations et d'inéquations
avec une fonction tangente
1. Résolution d'équations
On sait que les solutions de l'équation
tan X = a
sont
X = Arctan (a) + k π ,
k ℤ ℤ
2.Exemple
On veut résoudre l'équation:
- 2 tan((1/2)(x - π)) + 2 = 0
tan((1/2)(x - π)) = 2/2 = 1
D'où:
(1/2)(x - π) = tan-1(1) + kπ,
k ℤ ℤ
(1/2)(x - π) = π/4 + kπ
x - π = π/2 + 2kπ
x = π + π/2 + 2kπ
x = 3π/2 + 2kπ,
k  ℤ ℤ
3.Inéquation
Une inéquation de type :
a tan (b(x - h)) + k ≥ s
Conduit à résoudre l'inéquation:
tan (b(x - h)) ≥ (s - k)/a
• Méthode graphique:
Une représentation graphique est toujours utile.
1) Tracer a droite horizontale y = (s - k)/a
2) Tracer le graphe de la fonction g(x) = tan (b(x - h))
3) Comparer.
• Méthode algébrique:
À l'intérieur d'une période:
• Si b ≥ 0, la fonction g(x) = tan (b(x - h))
est croissante
tan (b(x - h)) ≥ (s - k)/a -> b(x - h) ≥ Arctan((s - k)/a)
• Si b ≤ 0, la fonction g(x) = tan (b(x - h))
est décroissante
tan (b(x - h)) ≥ (s - k)/a -> b(x - h) ≤ Arctan((s - k)/a)
4. Exemple
Soit à résoudre l'inéquation:
- 3 tan ((1/2)(x - π)) + 2 ≤ 5
Nous avons:
- 3 tan (b(x - h)) ≤ 3
Simplifiée, l'inéquation devient:
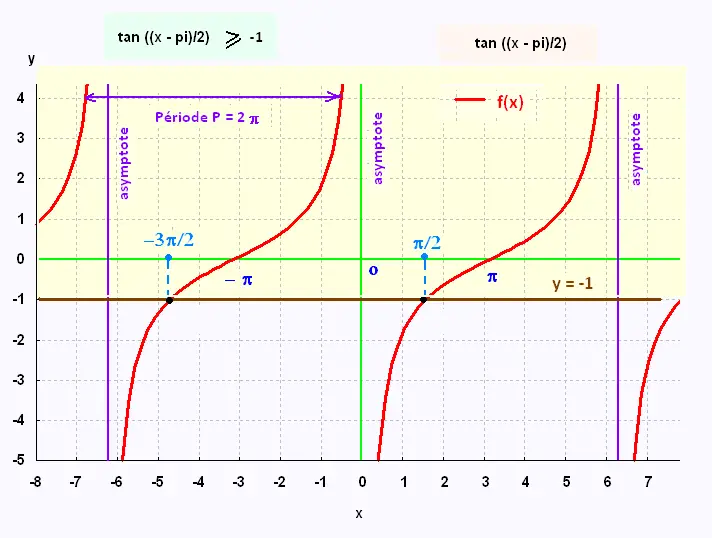
tan ((1/2)(x - π)) ≥ - 1
On considère donc la fonction
g(x) = tan ((1/2)(x - π))
P = π/|(1/2)| = 2π
L'ensemble solution dans une période est :
S = [- 3π/2, 0[ .
L'ensemble solution complet est:
S = [- 3π/2 + kP, 0 + kP[ , soit:
S = [- 3π/2 + 2kπ, 2kπ[
k ℤ ℤ
Algébriquement:
b ≥ 0, la fonction est donc croissante dans
une période. D'où:
tan ((1/2)(x - π)) ≥ - 1
-> (1/2)(x - π) ≥ - π/4
-> x - π ≥ - π/2
-> x ≥ π/2 .
Donc
S = [π/2 , 2π[ .
S = [π/2 + 2kπ, 2kπ[
,
k ℤ ℤ
Qui est équivalent à celui trouvé graphiquement.
|
|