Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre & Géométrie
Les fonctions trigonométriques
La fonction tangente
Règle de la fonction tangente
1. Les paramètres importants
• Sous forme canonique, l'équation de
la fonction tangente est:
f(x) = a tan (b(x - h)) + k
• La période de la fonction tangente est:
P = π/|b|
• Équation des asymptotes :
x = h + (n + 1/2)P.
• Si x1 et x2 sont deux équations
de deux symptotes consécutives , alors;
x2 - x1 = [h + (n + 1 + 1/2)P] - [h + (n + 1/2)P] = P.
Ainsi la différence des deux abscisses de deux
asymptotes consécutives donne la valeur de la période.
P = Δ(asymptotes consécutives)
• Si x1 et x2 sont deux équations
de deux symptotes consécutives , alors
leur cosinus est nul. C'est à dire :
a cos(b(x1 - h)) + k = a cos(b(x2 - h)) + k = 0.
D'où: h = (x1 + x2)/2
h = (x1 + x2)/2
Ainsi la moyenne des deux abscisses de deux
asymptotes consécutives donne la valeur du paramètre h.
2. Exemple
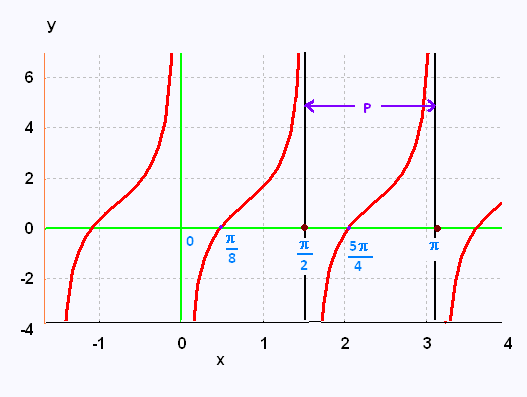
On demande de trouver la règle d'une fonction tangente ayant
deux asymptotes définies par les équations x = π/2
et x = π.
Entre ces deux asymptotes, le graphique de
la fonction passe par les points (π/8,0) et (3π/4, 1).
• La période P = π - π/2 = π/2.
D'où |b| = π/P = π/(π/2) = 2
On prend b > 0 pour l'instant. son signe sera déterminé
par le paramètre a.
• b = 2
• Le paramètre h = (π + π/2)/2 = 3π/4
h = 3π/4
• Au point (3π/4, 1):
f(3π/4 = 1 -> a tan (2(3π/4 - 3π/4)) + k = 1
a tan (0) + k = 1 .
D'où k = 1
k = 1
• Au point (π/8, 0):
f(π/8) = 0 -> a tan (2(π/8 - 3π/4)) + k = 0
a tan (- 5π/4 ) + k = 0
tan (- 5π/4) = - k/a.
La fonction tan est impaire ->
tan (5π/4) = k/a .
En substituant la valeur de k, on aura:
tan (5π/4) = 1/a . D'où
a = 1/tan (5π/4)
a = 1/tan (5π/4) = 1/tan (π/4) = 2/√2 = √2
a = √2
Au point π/8) = 0, la fonction est croissante
donc ab > 0 donc b est > 0.
Finalement, la règle de la fonction tangenet cherchée
est donc:
f(x) = √2 tan (2(x - 3π/4)) + 1
|
|