Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Fonction valeur absolue
Inéquations avec valeur absolue
Inéquations avec valeur absolue
1. Exemple
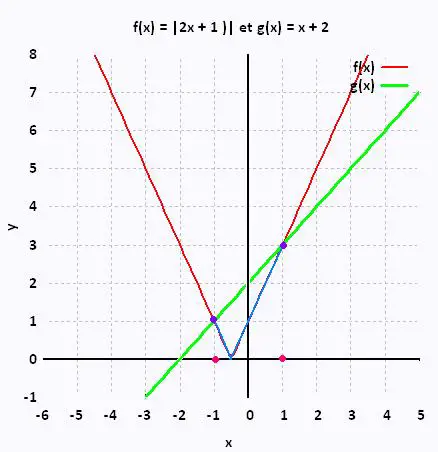
On veut résoudre l'inéquation
|2x + 1| ≤ x + 2.
Ici, nous avons une contrainte pour le membre de droite. Il
doit être positif ou nul.
D'après la définition de la valeur absolue, on a:
\[ \bf\color{brown}{
\lvert \text{2x + 1} \rvert =
\begin{cases}
+ \; \text{(2x + 1)} \; & \text{si} \qquad x \ge \; - 1/2 \\[2ex]
- \; \text {(2x + 1)} \; & \text{si} \qquad x \lt - 1/2
\end{cases}
}
\]
• Contrainte: x + 2 ≥ 0 → x ≥ - 2
• Branche de droite x ≥ - 1/2
2x + 1 ≤ x + 2 → x ≤ 1
L'intersection de ]- ∞, 1] , [- 1/2, ∞[ et [- 2, +∞[
est [- 1/2,1] .
La réponse convient.
• Branche de gauche x < - 1/2
- 2x - 1 ≤ x + 2 → x ≥ - 1
L'intersection [- 1, + ∞ ], ]- ∞, - 1/2[ , et [- 2, +∞[
est [- 1, - 1/2[ .
La réponse convient.
L'union des deux réponses constitue l'ensemnble des
solutions:
S = [- 1, 1]
2. Cas général
• |ax + b| ≤ C
Dans l'inéquation |ax + b| ≤ C,
C est soumis à la contrainte
d'être toujours positif.
ax + b ≤ c si ax + b ≥ 0
-(ax + b) ≤ c ou ax + b ≥ - c si ax + b < 0
On résoud donc les inéquations
ax + b ≤ c et
ax + b ≥ - c.
La solution finale est l'ensemble-solution formé par
l'union des solutions des deux inéquations
• |ax + b| ≥ C
Dans l'inéquation |ax + b| ≥ C,
C n'est soumis à aucune contrainte.
Il peut être positif ou négatif ou nul.
ax + b ≥ c si ax + b ≥ 0
-(ax + b) ≥ c ou ax + b ≤ - c si ax + b < 0
On résoud donc les inéquations
ax + b ≥ c et
ax + b ≤ - c.
La solution finale est l'ensemble-solution formé par
l'union des solutions des deux inéquations
3. Exemple
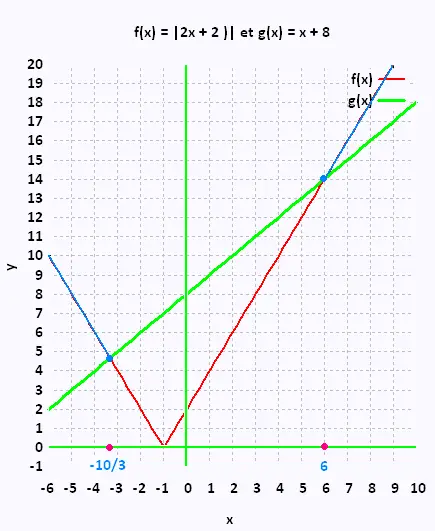
On veut résoudre l'inéquation
|2x + 2| ≥ x + 8 .
Ici, aucune contrainte pour le membre de droite. Il
peut être positif ou négatif ou nul .
D'après la définition de la valeur absolue, on a:
\[ \bf\color{brown}{
\lvert \text{2x + 2} \rvert =
\begin{cases}
+ \; \text{(2x + 2)} \; & \text{si} \qquad x \ge \; - 1 \\[2ex]
- \; \text {(2x + 2)} \; & \text{si} \qquad x \lt - 1
\end{cases}
}
\]
• Branche de droite x ≥ - 1
2x + 2 ≥ x + 8 → x ≥ 6
L'intersection de [- 1 , ∞[ et [6, ∞[
est [6, ∞[ .
La réponse convient.
• Branche de gauche x < - 1
- 2x - 2 ≥ x + 8 → x ≤ - 10/3
L'intersection ]- ∞, - 1[ , et [- ∞, - 10/3[
est ]- ∞, - 10/3[ .
La réponse convient.
L'union des deux réponses constitue l'ensemnble des
solutions:
S = ]- ∞, - 10/3[ ∪ [6, ∞[
|
|