Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Algèbre
La fonction logarithmique
Bürgi, les premières approches
Neper et le logarithme
Henry Briggs , le log
Neper et le logarithme

John Napier, connu en France sous le nom de Neper, est un mathéamaticien
et inventeur écossais.Il est né à Edimbourg , en Ecosse, en 1550 et y meurt
en 1617.
Napier ne possèdait aucune formation universitaire académique officielle
en Mathématique. Il les pratique en loisir et surtout à développement des
méthodes, aussi bien que des baguettes aidant à calculer.
Sa plus grande découverte est les logarithmes. En son honneur, on appelle le
logarithme à base e, ou logarithme naturel le logarithme néperien.
Neper s'intéressait à la recherche de nouvelles méthodes de calcul numérique
destinées à simplifier les calculs de trigonométrie
sphérique, alors essentiels pour l'astronomie et la navigation.
Il est aussi célèbre pour la création de la virgule, remplacée par le point
pour représenter un nombre décimal, et pour inventer des bagettes ou bâtons.
Ces bagettes de Napier est un instrument de calcul pour effectuer des multiplications,
des divisions, des racines carrées et cubiques. Cet instrument est à la
base de la règle à calcul .
Les logarithmes apparaissent en 1614 dans le livre de Neper
"Mirifici Logarithmorum Canonis Descriptio". Le terme logarithme
du grec logos: rapport , ou proportion et arithmos: nombre.
Le logarithme est alors le rapport de deux nombres.
Dans le deuxième traité " Mirifici Logarithmorum Canonis Constructio", en 1619,
l'objectif était de simplifier les calculs trigonométriques de l'astronomie en
remplaçant les multiplications et divisions par des additions et soustractions.
Dans le but de substituer l'addition à la multiplication, il met des liens entre
les termes de la progression géométrique et ceux de la progression arithmétique.
C'est ainsi qu'il découvre les logarithmes.
Partant de la relation trigonométrique: sin(a) sin(b) = (1/2) cos(a - b) - (1/2) cos(a + b)
dans laquelle un produit de deux facteurs s'exprime comme somme de deux termes, Neper cherche
une suite similaire de nombres telle que le produit de deux de ces
nombres puisse s'exprimer à l'aide de leur somme.
Pour cela, il construit, à l'aide de la cinématique, deux suites de nombres telles que
l'une croît dans une progression arithmétique pendant que l'autre décroît dans une
progression géométrique.
À l'origine donc, Néper définit le logarithme comme le rapport de la distance à parcourir
de deux mobiles, l’un se déplaçant à vitesse constante et l’autre à vitesse
proportionnelle à la distance restant à parcourir. Les sécances respectives
sont une progression arithmétique et une progression géométrique.
Dans son ouvrage "Mirifici logarithmorum canonis descriptio" (1614),
publie ses recherches qui contient également une table des
logarithmes des sinus d'angles croissants de minute en minute.
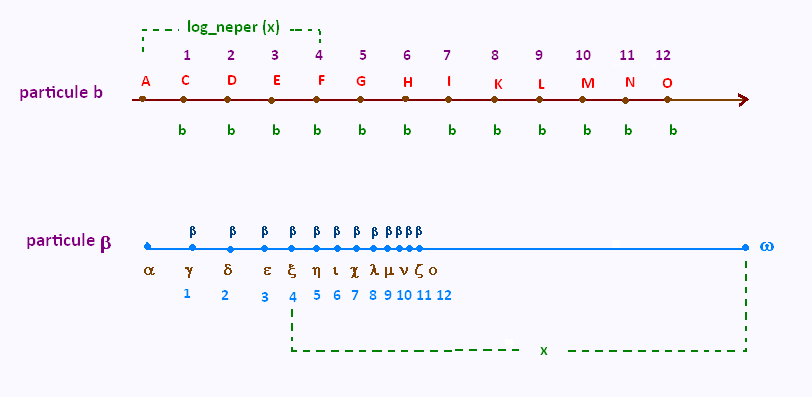
Napier bâtit sa conception du logarithme dans un cadre cinématique. Napier a imaginé deux
particules se déplaçant le long de deux lignes parallèles.
Ces deux particules partent en même temps, du même point, avec la même vitesse. La première particule se déplace en mouvement uniforme sur la ligne d'une longueur infinie de sorte qu'elle couvre des distances égales en des temps égaux. La seconde particule se déplace sur un segment de droite fini alors que sa vitesse est proportionnelle à la distance restante au point terminal.
À chaque instant, la distance restante à parcourir pour la particule β sur la ligne fini est le sinus d'un angle. La distance parcourue par la particule b sur la première (infini) ligne est le logarithme de ce sinus.
Le résultat est que les sinus ont diminué, les logarithmes de Napier augmenté. En outre, les sinus ont diminué en proportion géométrique, et les logarithmes augmenté en proportion arithmétique.
Napier utilisait donc la relation Pn+1 = Pn (1 - 1/107) =
P0 (1 - 1/107)n avec P0 chosisi = 107 = 10, 000, 000.0000000, qui est la distance du segment de longueur finie, trajet de la particule β.
Pour une progression arithmétique de raison a = 1, le logarithme de neper n passe de n à n + 1,
tandis que pour la progression géométrique de raison g = 1 - 1/107, les Pn passent de Pn à g x Pn. Le logarithme de neper log_neper, selon lequel
ses tables sont construites, est calculé selon la formule:
n = log_neper (Pn)
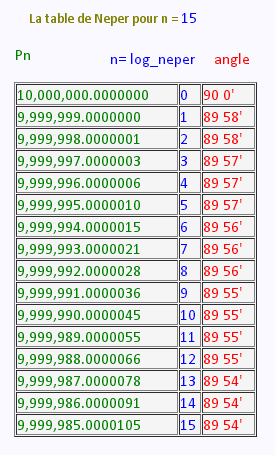
Jusqu'à la valeur de n = 15, par exemple, il obtient la table suivante:
AC = log_neper (γω)
AD = log_neper (δω)
AC = log_neper (εω)
Puis, à chacune des valeurs, Neper associe de minutes en minutes, un angle dont
107 fois le sinus correspond à la valeur de Pn.
Pour n = 15, on aura la table suivante:
Napier a tabulé ses logarithmes de 0o à 45o en minutes d'arc,
puis par symétrie, fourni les valeurs pour l'ensemble du premier quadrant.
Pour compléter ses tables, Neper a calculé près de dix millions d'entrées à partir
desquelles il a choisi les valeurs appropriées. Napier lui-même estimait que le calcul de
ce nombre d'entrées lui avaient pris vingt ans.
Les deux suites, arithmétique et géométrique, que Neper a
utilisées correspondant à des distances parcourues par des points mobiles.
L'exposant utilisé, qui est une quantité liée au temps, est une variable réelle. C'est aussi
une des avancées de Neper est d’avoir pensé et utilisé un exposant qui n’est pas
un entier mais qui est une variable réelle.
Les logarithmes crées par Neper ne sont pas tout à fait les logarithmes que
nous nommons aujourd’hui. En Ecosse, en 1614, en mathématiques, les notions de fonction,
de dérivée, d'exponentielle étaient inconnues et même l’écriture
des nombres décimaux était très récente et pas encore fixée avant Neper.
A cette époque, on utilisait, des fractions au lieu décrire des chiffres à droite de la
virgule.
On note bien que Neper n'utilsait ni les puissances
ni les exposants, mais seulement deux progressions en relation,
l’une géométrique, l’autre arithmétique.
Si on attribue une base au logarithme de Neper, elle sera la suivante:
À partir de la relation: n = log_neper (Pn) où
Pn = P0(1 - 1/107)n
avec P0 chosisi = 107, on en déduit
log_neper (Pn) = n log_neper (P0(1 - 1/107)).
D`où: log_neper (P0(1 - 1/107)) et donc
P0(1 - 1/107) est la base de Neper. Elle vaut :
107(1 - 1/107) = 107 - 1 = 9999999.0000000
En termes modernes, nous pouvons dire que la base du logarithme dans la table de Napier
est :
base_neper =
(1 - 1/107)107
La relation qui existe entre le logarithme de Neper (log_neper(x))
et le logarithme népérien ln (x) = loge (x) est:
log_neper(x) = 107 ln(107/x)
Voici une des tables de Neper:
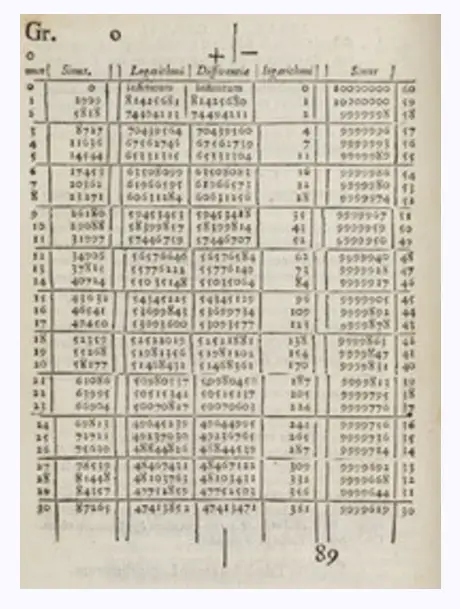
(
Références: www.ssplprints.com
)
Napier a démontré souvent les avantages de sa méthode. Par exemple, il a travaillé à
travers un problème impliquant le calcul des moyennes proportionnelles, parfois
connu comme la moyenne géométrique.
Il a souligné que sa technique en utilisant
les logarithmes trouve non seulement la réponse, plus vite, mais utilise seulement
une addition et une division par deux. Il considère alors les
extrêmes 1000000 et 500000 .
La moyenne proportionnelle recherchée: qui est
communément trouvée en multipliant les extreames donnés, l'un par l'autre, et
et en en extrayant la racine carrée du produit, peut se faire plustôt ainsi en
ajoutant leurs logarithmes respectifs 0 et 693147, qui est 693147 et en la
divisant par 2 et le quotient obtenu est 346.573 qui est le logarithme de la moyenne
proportionnelle désirée qui donne 707.107, et ses arc de 45 degrés trouvés trouvé par addition
seulement par une addition et une division par deux.
• sqrt(1000000 x 500000) = 707106.78
• log_neper(1000000) + log_neper(500000) =
0 + 693147 (tirées de sa table) = 693147
• 693147 / 2 = 346573
• De nouveau à partir de sa table le nombre 346573 , qui est un logarithm,
correspond au nombre 707107, comme demandé,
• qu'il jugeait à juste titre était beaucoup plus simple à calculer.
|
|