Mathématiques 2:

Fonction racine carrée
Inéquations avec racine carrée

1. La méthode

Pour résoudre une inéquation avec une racine carré, on procède de la façon suivante selon 5 étapes:

• Isoler la fonction racine carrée,
• Tenir compte des DEUX contraintes:
      . le radicande est positif,
      . le radical est positif, puis
      . former l'intervalle des contraintes par intersection,
• Résoudre l'inéquation en élévant au carré ses deux membres,
• Vérifier la validité de chaque réponse dans l'intervalle
des contraintes ,
• Donner la réponse finale par l'union des ensembles solutions de chaque réponse.

2. Cas simples

Une fois le radical isolé, on aura:

$\bf \sqrt {a x + b} \le c \text { or } \ge c \text{ or } \gt c \text{ or } \lt c$

• $\bf \sqrt {a x + b} \le c$
Si c est négatif l'inéquation est impossible S = { }.

• $\bf \sqrt {a x + b} \ge c \text { ou } \gt c$
Si c est négatif l'inéquation se réduit à $\bf \sqrt {a x + b} \ge 0$

3. Exemples

Exemple 1

Résoudre l'inéquation suivante :

\[ \bf\large \sqrt {\textit 2x + 1} - 3 \le 1 \]
$\bf\color{brown}{ \sqrt {2x + 1} \le 4 }$

2x + 1 ≥ 0 . Donc x ≥ - 1/2
l'intervalle de définition est alors:
D = [-1/2, + ∞[

$\sqrt {2x + 1} \le 4 \\ 2x + 1 \le 16 \\ x \le \frac{15}{2} \\ $
L'ensemble solution est donc:
So = ]- ∞, 15/2]
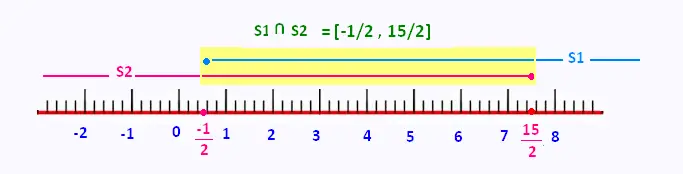
L'ensemble final des solutions est donc S = D ∩ So
S = [- 1/2, 15/2]

Exemple 2

Résoudre l'inéquation suivante :

\[ \bf\large \frac{5}{3}\sqrt {-\frac{3}{4} (x - 6)} + \frac{5}{2} \ge 0 \] $\bf \frac{5}{3}\sqrt {-\frac{3}{4} (x - 6)} \ge - \frac{5}{2}$

$\bf \sqrt {- \frac{3}{4} (x - 6)} \ge - \frac{3}{2}$

$c = - \frac{3}{2}$ est négatif l'inéquation se réduit donc à \[ \bf\large \sqrt {-\frac{3}{4} (x - 6)} \ge 0 \]
$-\frac{3}{4} (x - 6) \ge 0 \\ (x - 6) \le 0 \\ \text { } \\ \bf\large x \le 6$

L'ensemble solution se confond avec le domaine de définition qui est ici l'un des domaines des contrantes:

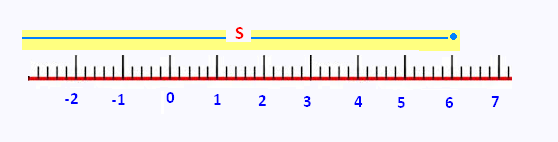
S = ]- ∞, 6]