Mathématiques 2:

Fonction racine carrée
Fonction racine carrée de base

1. Définition

La racine carrée d'un nombre réel positif x est le
nombre réel positif a dont le carré a² donne x:

La fonction racine carrée ne manipule que des nombres positifs. le radical $\sqrt {}$ est strictement réservé à cette fonction. La fonction valeur absolue ne connaît pas de signe.

Lorsqu'un terrain carré a une aire de 81 m², son côté est donc égal à $\sqrt{81} = 9 \;m.$

$\sqrt{81} \ne \pm \; {9}$, puisque la racine carrée ne manipule que des nombres positifs sans signe. On s'entend sur $\sqrt{81} \equiv \; {9}.$

Si l'on veut la vraie définition de la racine carrée, c'est la suivante:
$$\large \sqrt{x^2} = \left\lvert x \right\rvert$$
Bien entendu l'ecriture x² = 81 n'est pas nécessairement liée à une racine carrée. L'expression littérale x² = 81 est une équation du second degré à résoudre , mais pas par racine carrée.

x² = 81 → x² - 81 = 0 → (x - 9)(x + 9) = 0,
d'ensemble-solution S = {- 9, + 9}

On obtient deux solutions: deux racines de l'équation et non deux racines carrées.

Pour une équation du second degré x² = a la racine carrée n'apparaît que si le nombre positif a n'est pas un carré parfait.

x² = 7 → $x^2 - (\sqrt{7})^2 \Rightarrow (x - \sqrt{7})(x + \sqrt{7})$
, d'ensemble-solution S = {- √7, + √7}



$\sqrt x$ = a       vraie si       x ≥ 0 ET a ≥ 0

f(x) = $\sqrt x$ est la fonction de base.

Dans l'ensemble des nombres réels ℝ $\sqrt x$ n'est pas définit si x < 0.

Exemple : $\sqrt {- 16 }$ n'existe pas.

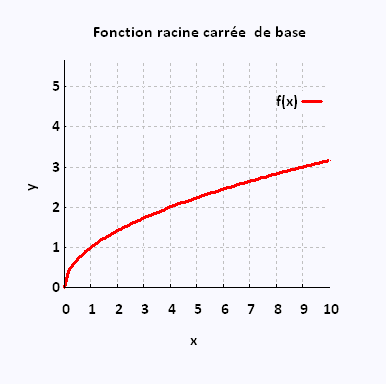
2. Graphique de la fonction racine carrée de base