Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Fonction valeur absolue
Valeur absolue avec du second degré
Valeur absolue avec du second degré
Exemple
On veut résoudre l'équation
|x2 + 5x | = 6 .
D'après la définition de la valeur absolue, on a:
|x2 + 5x | =
+ (x2 + 5x) si (x2 + 5x) ≥ 0
- (x2 + 5x) si (x2 + 5x) < 0
Les racines de l'équation x2 + 5x sont x = - 5 et x = 0 .
Le polynome x2 + 5x est :
• du signe de a (= + 1), donc
≥ 0 à l'extérieur des racines: ] - ∞, - 5] ∪ [0, + ∞ [
• du signe contraire de a (= + 1), donc
< 0 à l'intérieur des racines: ] - 5, 0[
Ainsi :
|x2 + 5x | =
x2 + 5x dans
] - ∞, - 5] ∪ [0, + ∞ [
- x2 - 5x dans
] - 5, 0[
• dans
I1 = ] - ∞, - 5] ∪ [0, + ∞ [ :
x2 + 5x = 6
x2 + 5x - 6 = 0
→ x1 = - 6, x2 = 1
Les réponses conviennent
puisqu'elles se trouvent dans I1 .
• dans
I2 = ] - 5, 0[ :
- (x2 + 5x) = 6
x2 + 5x + 6 = 0 → x3 = - 3 , x4 = - 2
Les réponses conviennent
puisqu'elles se trouvent dans I2 .
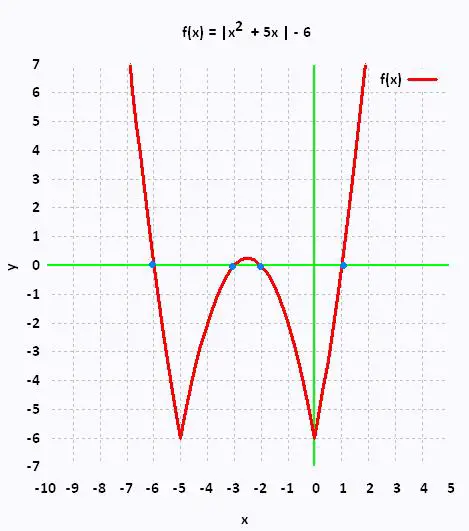
L'ensemble des solutions est donc
S = {- 6, - 3, - 2, 1}
|
|