Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
INÉQUATIONS AVEC DES VALEURS ABSOLUES
Exercice 1
Résoudre dans R l’équation suivante :
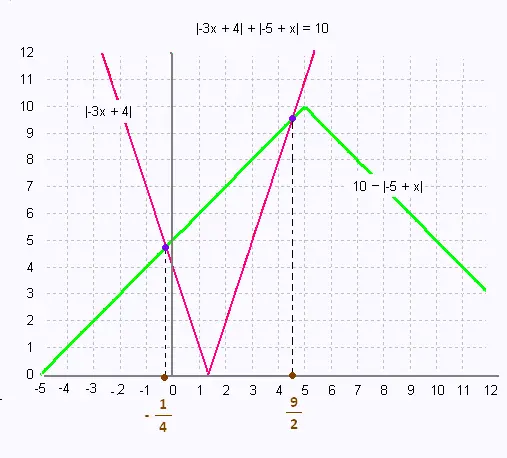
|-3x + 4| + |-5 + x| = 10 (E)
 ↓Réponse↑ ↓Réponse↑
On détermine les valeurs frontières de chaque valeur absolue :
• 3x + 4 = 0 soit x = 4/3
• 5 + x = 0 soit x = 5
On remplit un tableau de forme :
| x |
- ∞ |
|
4/3 |
|
5 |
|
+∞ |
| |-3x + 4| |
|
- 3x + 4 |
0 |
3x - 4 |
11 |
3x - 4 |
|
| |-5 + x| |
|
5 - x |
11/3 |
5 - x |
0 |
- 5 + x |
|
| (E) |
|
-4x+9 = 10 |
| |
2x + 1 = 10 |
| |
4x - 9 = 10 |
|
| |
|
x = -1/4
possible |
| |
x = 9/2
possible |
| |
x = 19/4
impossible |
|
On obtient alors deux solutions S =
(- 9/4; 9/2)
Résolution graphique:
Exercice 2
Résoudre dans R l’inéquation suivante :
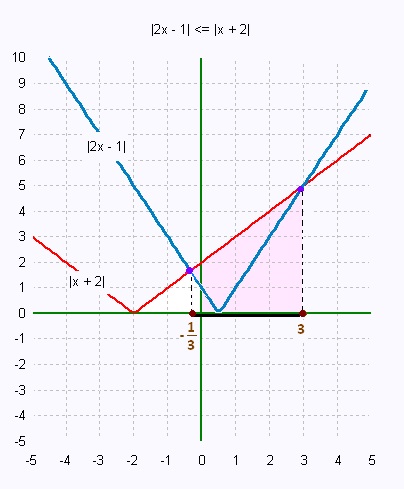
|2x - 1| ≤ |x + 2|
 ↓Réponse↑ ↓Réponse↑
On détermine les valeurs frontières de chaque valeur absolue :
• 2x - 1 = 0 soit x = 1/2
• x + 2 = 0 soit x = -2
On remplit un tableau de forme :
| x |
|
-2 |
|
1/2 |
|
| |x + 2| |
- x - 2 |
0 |
x + 2 |
|
x + 2 |
| |2x - 1| |
-2 x + 1 |
|
- 2x + 1 |
0 |
2x - 1 |
| |2x - 1| ≤ |x + 2| |
- x + 3 ≤ 0 |
| |
-3 x - 1 ≤ 0 |
| |
x - 3 ≤ 0 |
| |
x ≥ 3:
impossible |
| |
x ≥ -1/3:
possible dans: [-1/3, 1/2] |
| |
x ≤ 3 :
possible dans: [1/2, 3] |
On obtient alors l'intervalle de solutions S =
[-1/3, 3].
Résolution graphique:
Exercice 3
Résoudre dans R l'inéquation;
|3x - 1| ≥ x - 2
 ↓Réponse↑ ↓Réponse↑
3x - 1 = 0, soit x = 1/3
|3x - 1| s'écrit:
- 3 x + 1 avec x ≤ 1/3
3 x - 1 avec x ≥ 1/3
L'inéquation s'écrit donc:
- 3 x + 1 = x - 2 avec x ≤ 1/3
x = 3/4 avec x ≤ 1/3 : impossible
3 x - 1 = x - 2 avec x ≥ 1/3
x = - 1/2 avec x ≥ 1/3 : impossible
Il n'y a pas de solution.
L'équation n'admet aucune solution dans R.
Exercice 4
a) Résoudre l'inéquation
|2x + 1| ≤ |x - 1|
b) L'inéquation est équivalente à
(2x + 1)2 - (x - 1)2 ≤ 0 (INEQ)
Justifier cette affirmation et
résoudre l'équation.
 ↓Réponse↑ ↓Réponse↑
a)
| x |
|
-1/2 |
|
1 |
|
| |2x + 1| |
- 2x - 1 |
0 |
2x + 1 |
|
2x + 1 |
| |x - 1| |
- x + 1 |
|
- x + 1 |
0 |
x - 1 |
| (INEQ) |
- x - 2 ≤ 0 |
| |
3 x ≤ 0 |
| |
x + 2 ≤ 0 |
| |
x ≥ - 2:
possible |
| |
x ≤ 0
possible |
| |
x ≤ - 2
impossible |
L'ensemble des solutions est S = [- 2, 0].
b) selon la propriété:
si a et b sont des réels positifs et
a ≤ b , alors a 2 ≤ b 2
Ainsi:
|2x + 1| ≤ |x - 1| peut bien s'ecrire :
(2x + 1) 2 ≤ (x - 1) 2
Les expressions:
|2x + 1| ≤ |x - 1| et (2x + 1) 2 - (x - 1) 2 ≤ 0
sont équivalentes:
Noua avons:
(2x + 1) 2 - (x - 1) 2 = (3x)(x + 2)
L'inéquation devient:
3 x ( x + 2) ≤ 0 (INEQ)
On fait un tableau de signe: :
| x |
- ∞ |
|
- 2 |
|
0 |
|
+∞ |
| x + 2 |
- |
- |
0 |
+ |
| |
+ |
+ |
| 3x |
- |
- |
- |
- |
0 |
+ |
+ |
| (INEQ) |
+ |
+ |
| |
- |
| |
+ |
+ |
| |
|
|
| |
ici |
| |
|
|
L'ensemble des solutions est S = [- 2, 0].
|
|