Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Fonction valeur absolue
Forme canonique de la valeur absolue
Forme canonique de la valeur absolue
1. Définitions
La forme canonique de la fonction valeur absolue est :
y = a|b(x - h)| + k
En utilisant la propriété |x y| = |x| |y|, le paramètre b peut
sortir de la valeur absolue et l'on a:
y = a|b||x - h| + k
On obtient alors la forme à trois paramètres suivante:
y = a1|x - h| + k
avec
a1 = a|b|
2. Exemples
• Exemple 1
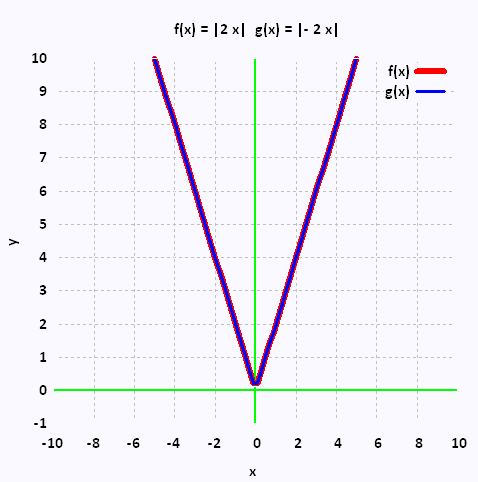
f(x) = 2 | x |
a = 2, b = 1 , h = 0 , k = 0
g(x) = 2 | - x |
a = 2, b = - 1 , h = 0 , k = 0
Nous avons
g(x) = 2 |- 1| |x| = 2 |x| = f(x)
Le produit a |b| est le même pour b positif ou négatif.
Ainsi, la fonction |2 x| est identique à la fonction |- 2 x|
• Exemple 2
f(x) = |3 x| a = 1 et b = 3
g(x) = 3 |x| a = 3 et b = 1
|3 x| = 3 |x|
Ainsi les expressions |3 x| et 3|x| sont équivalentes.
Les fonctions f(x) et g(x) sont identiques.
• Exemple 3
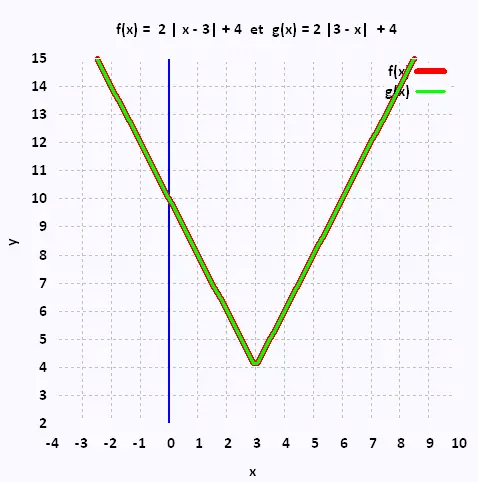
f(x) = 2 |x - 3| + 4
a = 2, b = 1 , h = 3 , k = 4
g(x) = 2 |3 - x | + 4
On transforme d'abord l'expression de g(x) en
la forme canonique y = a |b(x - h)| + k. Donc
g(x) = 2 | - (x - 3)| + 4.
a = 2, b = - 1 , h = 3 , k = 4
Selon la propriété |x . y | = |x| . |y|, on a
g(x) = 2 | - 1| |(x - 3)| + 4
g(x) = 2 |x - 3| + 4
a = 2, b = 1 , h = 3 , k = 4
Ainsi, la fonction f(x) = 2 |x - 3| + 4 est identique à la
fonction g(x) = 2 |3 - x | + 4.
|
|