Mathématiques
2
Mathématiques
Sde - SN5
Fonction valeur absolue
Fonction racine carrée
Fonction rationnelle
Fonction exponentielle
Fonction logarithmique
Fonctions trigonométriques
Fonction sinusoidale
Fonction tangente
Applications
Exercices
Calculateurs
© The scientific sentence. 2010
|
Mathématiques:
Fonction valeur absolue
Équation d'une fonction valeur absolue
Trouver l'équation d'une fonction valeur absolue
1. Exemple
Trouver l'équation de la fonction valeur absolue ayant son
sommet au point de coordonnées (3, - 2) et passant par le point
(- 1,6).
Nous avons h = 3 et k = - 2 qui sont les coordonnées du sommet.
Donc f(x) = a1 |x - 3| - 2
Le point (- 1, 6) vérifie l'équation f(x). D'où:
f(- 1) = 6 = a1 |- 1 - 3| - 2 = 4 a1 - 2
4 a1 - 2 = 6 → a1 = 2 .
L'équation cherchée est:
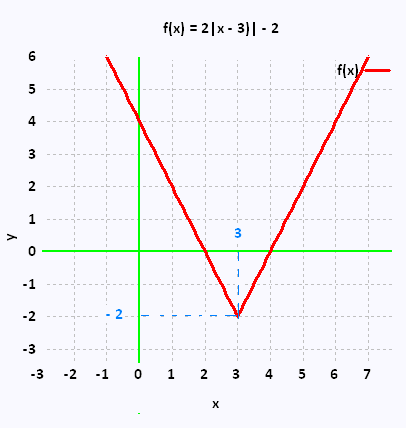
f(x) = 2 |x - 3| - 2
• Remarque:
Le calcul de la pente donne:
Pour deux points quelconques, soit (3, - 2) et (- 1,6), on aura:
Pente = Δy/δx = (6 + 2)/(- 1 - 3) = 8/(- 4) = - 2 ,
qui est la pente de la branche de gauche. Sachant que les pentes des deux branches
sont de valeurs opposées, on en déduit que la pente de la branche de droite,
c'est à dire le paramètre a1, vaut + 2.
2. Règle générale
Sous sa forme canonique à quatre paramètres la fonction valeur absolue s'ecrit:
f(x) = a |b(x - h)| + k = a |b| |x - h| + k.
Le produit a1 = a |b| représente la pente de la branche de droite de
la fonction f(x). - a1 représente la pente de la branche de gauche de
la fonction f(x).
La valeur de a1 est fixée. Ainsi pour former ce produit,
et b peut prendre une infinité de valeurs.
Pour trouver l'équation sous la forme canonique d'une valeur absolue, il suffit
de connaître les coordonnées du sommet et le taux de variation de la branche de droite.
On trouve ainsi la forme canonique à trois paramètres f(x) = a1 |x - h| + k. Cette
équation est unique.
|
|