Mathématiques:

Fonction valeur absolue
Popriétés

Propriétés de la fonction valeur absolue

Exemple et généralités

Propriété	Fonction	Exemple
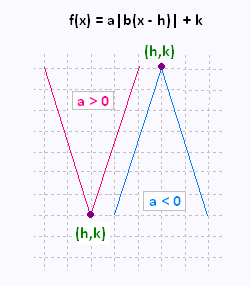
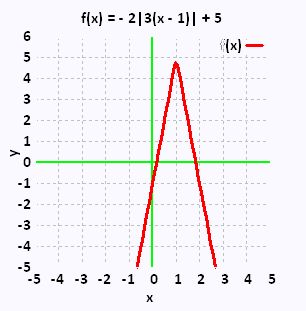
	f(x) = a |b(x - h)| + k = a1 |x- h| + k	f(x) = - 2|3(x - 1)| + 5 = - 6|x - 1| + 5
Coordonnées du sommet	(h, k)	(1,5)
Domaine (Dom f)	dom f = R	dom f = R
Image (Ima f)	• Si a > 0, les images sont définies dans ]k, + ∞ • Si a < 0, les images sont définies dans ]- ∞ , k[	Ima f = ]- ∞ , 5[
Variations	• Si a > 0, f(x) est croissante dans ]h, + ∞ [ , et decroissante dans ]- ∞ , h[ • Si a < 0, f(x) est decroissante dans ]h, + ∞ [ et croissante dans ]- ∞ , h[	• croissante dans ]- ∞ , 1[ • decroissante dans ]1, + ∞ [
Zéros de la fonction	Ce sont les valeurs de z1 et z2 de x tels que f(x) = 0. S'ils existent.	Les zéros sont : z1 = 1/6 et z2 = 11/6
Ordonnée à l'origine	Valeur de f(x = 0)	f(0) = - 1
Signe de la fonction f	• Si a > 0, f(x) est positive dans ]- ∞, z1[ ∪ [z2, ∞[ , et negative dans ]z1, z2[ • Si a < 0, f(x) est positive dans [z1, z2] et négative dans ]- ∞, z1[ ∪ [z2, ∞[	a1 = - 6 < 0, f(x) est positive dans [1/6, 11/6 ] et négative dans ]- ∞, 1/6[ ∪ ]11/6, ∞[
Extremums	• Si a > 0, la valeur minimale est k. • Si a < 0, la valeur maximale est k.	• a1 < 0, la valeur maximale est 5.
Équation de l'axe de symétrie	x = h	x = 1
Graphique de la fonction

Pour imprimer un modèle de table des propriétés d'une fonction valeur absolue : table des propriétés