Combinatorics
Probability & Statistics
© The scientific sentence. 2010
|
Gaussian distribution
We will set the normal distribution from
the binomial distribution:
P(x) = n!/x!(n - x)! pxqn - x
An approximation to this binomial distribution for large n
can be obtained by expanding about the value μ where P(x)
is a maximum, i.e., where dP/dx=0.
Let write x = μ + ζ and use the Maclaurin series around
ln P(μ):
ln P(x) = ln P(μ) + ζ d/dx [ln P(x)] + (1/2)ζ2 d2/dx2[ln P(x)] + ...
ln P(x) = ln n! - ln x! - ln (n-x)! + x ln p +(n - x) ln q
Using stirling approximation:
ln y! &asym; y ln y - y, we have:
ln P(x) = n ln n - n - x ln x! + x - (n-x) ln (n-x) + n - x + x ln p + (n - x)ln q
= n ln n - x ln x - (n-x)ln (n-x) + x ln p + (n - x)ln q
And:
d/dx [ln P(x)] = - ln x - 1 + 1 + ln(n-x) +ln p - ln q
= - ln x + ln(n - x) + ln p - ln q
This experssion must be equal to zero, because we are developping
around the maximum.
This condition gives us the mean:
d/dx [ln P(x)] = 0 ⇒ ln(n - x)/x = ln(q/p)
Since p+q = 1, we have the mean = μ = np
d2/dx2[ln P(x)] = -1 /x -1/(n-x)
With x = μ we have :
d2/dx2[ln P(x)] = -1/npq
The following terms get smaller. We can write:
ln P(x) = ln P(μ) + 0 -1/npq (1/2)ζ2, and
P(x) = P(μ) exp {-1/2npq ζ2}
Let' normalise this probability to 1:
∫ P(x) dx = 1
dx = dζ
1 = ∫ P(μ) exp {-1/2npqζ2} dζ [ζ: 0 → + ∞ ]
= (2npq)1/2 P(μ) ∫ (2npq&) exp {- ζ2} dζ
= (2npq)1/2 P(μ) (π)1/2
= (2npqπ)1/2 P(μ)
Hence:
P(μ) = 1/(2npqπ)1/2
Thus:
P(x) = 1/(2npqπ)1/2 exp {-1/2npq ζ2}
With:
ζ = x - μ and σ2 = npq ,
The Gaussian distribution:
P(x) = 1/σ(2π)1/2 exp {- (x - μ)2/σ2}
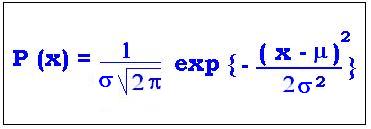
|
|
|