Combinatorics
Probability & Statistics
© The scientific sentence. 2010
|
Probability & statistics
1. Bernoulli trials
A Bernoulli process is a sequence of repeated trials
of an experiment in which:
- Each trial has two possible outcomes E and E (success or failure)
- The trials are indepenedent
- The probability p(E) of an event E is the same for each trial
Let's recall that a trial is independent means that it does
not depend on any other trials; that is the outcome of one trial
does not influence the outcome of any other trial.
If p(E) is the probability of succes; then, according to the complement
rule q = 1 - p(E) is the probability of failure.
The main purpose of the Bernoulli trials is to determine
the probability that an event E occurs exactly "r" times among
a series of "n" trials of a random experiment.
We can solve a problem by two approches:
1. Using a stochastic diagram
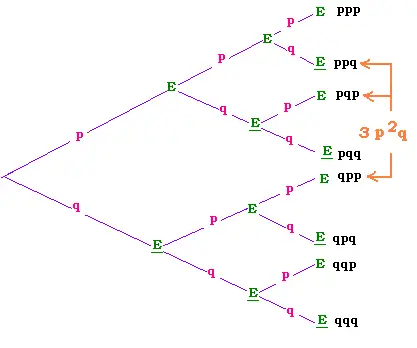 The probabilty to have "success" twice among three trials
is ppq or p2q. it occurs three times. We ad them
to have the total probability, that gives 3 p2q
(aal of the branches of the tree are mutually exclusive).
As we have seen the number three in 3 p2q is
a numer of combinations, that is C(2,3)=3. Finally, the
probability to have success twice is C(3,2)p2q.
2. Using the Binomial formula
1 = (p+q)N = = ∑ C(n,N)pnqN-n [n: 0 → N]
in which each term of the series represents the probability to
get "success" "n" times among N trials.
The collection {p(m,n), m = 1,2,3 ... n} forms a probability
distribution called the binomial distribution.
The probabilty to have "success" twice among three trials
is ppq or p2q. it occurs three times. We ad them
to have the total probability, that gives 3 p2q
(aal of the branches of the tree are mutually exclusive).
As we have seen the number three in 3 p2q is
a numer of combinations, that is C(2,3)=3. Finally, the
probability to have success twice is C(3,2)p2q.
2. Using the Binomial formula
1 = (p+q)N = = ∑ C(n,N)pnqN-n [n: 0 → N]
in which each term of the series represents the probability to
get "success" "n" times among N trials.
The collection {p(m,n), m = 1,2,3 ... n} forms a probability
distribution called the binomial distribution.
|
|
|