Counting analysis

1. Combinations

Let's consider again the following set of digits Set= {1,2,3}

Question1:
How many numbers of two digits can we obtain from 
this set?. The answer is:
12, 13, 21, 23, 31, and 32. In total, 6 numbers.

For every number with the same digits, we have exactly 2!=2 
repeatitions.

Question2:
How many numbers of two identical digits can we obtain from 
this set?. The answer is:
We have only three : 12, 13, 23

The order of these numbers IS important. The arragement 
13 and 31 , for example, are the same.

The question would be presented as: How many arrangements 
of two digits can we make from the three elements of the set Set, 
when the order is important?

There are 3 manners to arrange two digits among three digits acording 
this constraint.

We process as we did for the arragement. We arrange r objects among 
n objects with order. Here the arrangement is called comination:

Since we know the number of counts for arragements, we deduce 
the one for combinations. For every number with the same digits, 
we have  exactly !r repeatitions. We simply divide the number of 
arragements by n! to set the number of combinations. It follows:


The number of combinations of r among n objects is 
C(r,n) = A(r,n)/r! = n!/(n-r)! r!


C(r,n) gives also the number of r-subsets possible out of a set 
of n distinct elements. For example, The 2-subsets of {1,2,3} are 
the three pairs {1,2}, {1,3}, {2,3}, so C(2,3)=3.

2. Pascal triangle

The Pascal triangle can be constructed from the 
extantions of the binomials:

(a + b)0 = 1
(a + b)1 = 1 a1 +  1 b1
(a + b)2 = 1 a2 +  2 ab + 1 b1
(a + b)3 = 1 a3 +  3 a2b + 3 a b2 + 1 b3
(a + b)4 = 1 a4 +  4 a3b + 6 a2b2 +  
					 4 ab3 + 1 b4
(a + b)5 = 1 a5 +  ....


(a + b)0 = C(0,0)
(a + b)1 = C(0,1) a1 +  C(1,1) b1
(a + b)2 = C(0,2) a2 +  C(1,2) ab + C(2,2)b1
(a + b)3 = C(0,3) a3 +  C(1,3) a2b + C(2,3) a b2 + C(3,3)b3
(a + b)4 = C(0,4) a4 +  C(1,4) a3b + C(2,4) a2b2 +  
					  C(3,4) ab3 + C(3,4) b34
(a + b)5 = C(0,5)a5 +  .... + C(5,5)b5

That give the following general tringle: which includes 
the binomial coefficients


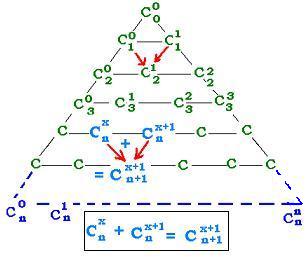We have the following relationship:

C(r+1,n) = (n-r)C(r,n)/(r+1)

C(r+1,n)  = n!/(n-r-1)!(r+1)! = n!(n-r)/(n-r)!(r)!(r+1) = 
(n-r)/(r+1) x n!/(n-r)!(r)! = (n-r)/(r+1) x C(r,n)