| Propriété |
Fonction (forme canonique) |
Exemple |
| |
f(x) = a sin (b(x - h)) + k = a cos (b(x - h) - π/2) + k
ou
g(x) = a cos(b(x - h)) + k = a sin (b(x - h) + π/2) + k
|
f(x) = - 3 sin(- 2(x - π)) + 1 |
| Équation de l'axe d'oscillation |
y = k |
y = 1 |
| Période |
P = 2π/|b| |
P = 2 π/|-2| = π |
| Domaine (dom f) |
dom f = R |
dom f = R |
| Image (Ima f) |
ima f = [k - |a|, k + |a|] |
ima f = [- 2, 4] |
| Variations |
• La fonction sinus f(x) est croissante au point (h,k) si a . b > 0.
Elle est décroissante en ce point si a . b. < 0.
• La fonction cosinus g(x) est croissante au point (h,k + a) si a > 0.
Elle est décroissante en ce point si a < 0.
|
Au point (π 1), la fonction sinus f(x) est croissante puisque
le produit ab = (- 3) (- 2) = + 6 est > 0.
|
| Zéros de la fonction |
Ce sont les valeures z de x, telles que
f(x) = 0.
Si x1 est une solution dans un cycle, alors
les autres zéros sont:
x = x1 + n P, et
x = π - x1 + n P, n  ℤ ℤ
|
- 3 sin(- 2(x - π)) + 1 = 0 -> sin(- 2(x - π)) = 1/3
- 2(x - π) = sin-1(1/3) -> x1 = (- 1/2)sin-1(1/3)
= 2.97 rad
La deuxième solution dans le cycle est x2 = π - 2.97 = 0.17 rad
-> Les zéro sont : z1 = 2.97 rad + n P = 2.97 rad + n π et
z2 = 0.17 rad + n π, n ℤ ℤ |
| Ordonnée à l'origine |
Valeur de f(x = 0) |
f(0) = - 3 sin(- 2(0 - π)) + 1 = 1
|
| Signe de la fonction f |
• f(x) est positive ou nulle dans
l'intervalle solution de l'équation f(x) ≥ 0.
• f(x) est négative dans
l'intervalle solution de l'équation f(x) < 0.
|
La fonction est négative (du signe de a) dans
[z1, z2] est positive ailleurs.
|
| Extremums |
• Maximum = k + |a|.
• Minimum = k - |a|
|
• Maximum = 1 + |-3| = 4
• Minimum = 1 - |-3| = - 2
|
| Graphique de la fonction |
|
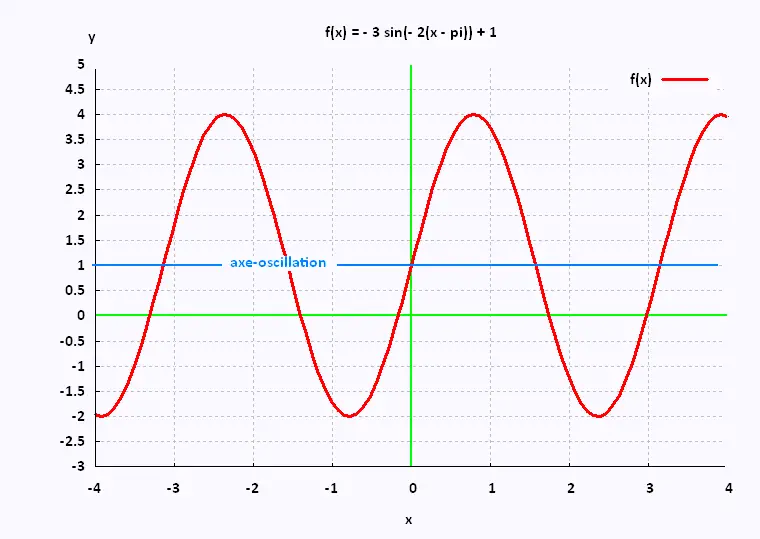
|