| Propriété |
Fonction (forme canonique) |
Exemple |
| |
f(x) = a tan (b(x - h)) + k
|
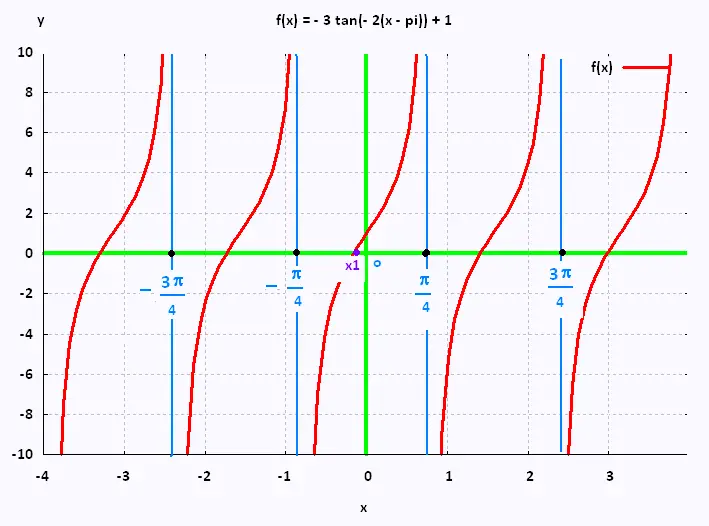
f(x) = - 3 tan(- 2(x - π)) + 1 |
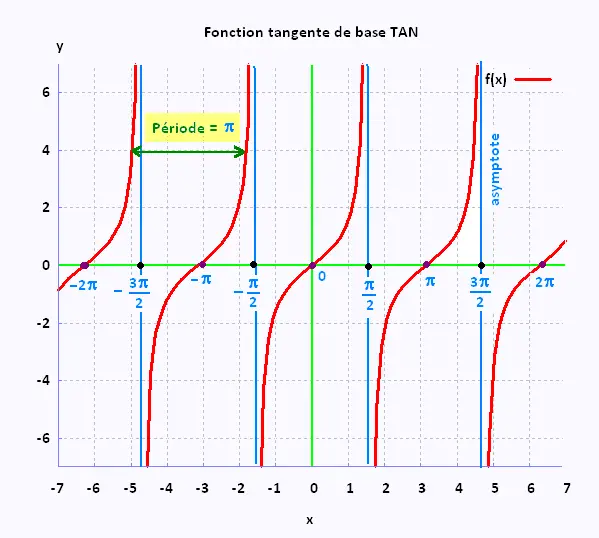
| Période |
P = π/|b| |
P = π/|-2| = π/2 |
| Équation des asymptotes |
x = h + (n + 1/2)P.
n ℤ |
x = π + (n + 1/2)π/2.
n ℤ
|
| Domaine (dom f) |
dom f = R\
{x/ x = h + (n + 1/2)P.
n ℤ
}
|
dom f = R\
{x/ x = π + (n + 1/2)π/2.
n ℤ
}
|
| Image (Ima f) |
ima f = R |
ima f = R |
| Variations |
• La fonction tangente f(x) est croissante entre deux
asymptotes consécutives si a . b > 0.
Elle est décroissante en cet intervalle si a . b. < 0.
|
Le produit (- 3)(- 2) = + 6 est > 0. Donc la fonction est
croissante entre deux asymptotes consécutives
|
| Zéros de la fonction |
Ce sont les valeures z de x, telles que
f(x) = 0. Si x1 est une solution dans un cycle, alors
les autres zéros sont: x = x1 + n P,
n ℤ
|
- 3 tan(- 2(x - π)) + 1 = 0 -> tan (- 2(x - π)) = 1/3
- 2(x - π) = tan-1(1/3) ->
x1 = (- 1/2)tan-1(1/3) + π = - 0.16 + π = 2.98 rad
-> x = x1 + nP.
x = 2.98 rad + nπ/2 ,
n ℤ
|
| Ordonnée à l'origine |
Valeur de f(x = 0) |
f(0) = - 3 tan(- 2(0 - π)) + 1 = 1
|
| Signe de la fonction f |
• f(x) est positive ou nulle dans
l'intervalle solution de l'équation f(x) ≥ 0.
• f(x) est négative dans
l'intervalle solution de l'équation f(x) < 0.
|
La fonction est positive dans
[x1 + nπ/2 , π/4 + nπ/2[ .
n ℤ .
Elle est négative ailleurs.
|
| Extremums |
• Aucun , sauf si le contexte limite le domaine ou l'image de la fonction
|
Aucun
|
| Graphique de la fonction |
|
|
table des propriétés