Mathématiques:

Fonction racine carrée
Popriétés

Propriétés de la fonction racine carrée

Exemple et généralités

Propriété	Fonction (forme canonique)	Exemple
	f(x) = a$\sqrt {b(x - h)}$ + k = a1$\sqrt {\pm (x - h)}$ + k	f(x) = 2$\sqrt {9(x + 5)}$ - 12 = 6$\sqrt {x + 5}$ - 12
Coordonnées du sommet	(h, k)	( - 5, - 12)
Domaine (Dom f)	• Si b > 0, dom f = [h, +∞[ • Si b < 0, dom f = ]- ∞, h[	[- 5, +∞[
Image (Ima f)	• Si a > 0, ima f = [k, + ∞ • Si a < 0, ima f = ]- ∞ , k]	Ima f = [- 12, +∞[
Variations	• Si a > 0 et b > 0, f(x) est croissante dans [h, + ∞ [ • Si a < 0 et b > 0, f(x) est décroissante dans [h, + ∞ [ • Si a > 0 et b < 0, f(x) est décroissante dans ]- ∞, h] • Si a < 0 et b < 0, f(x) est croissante dans ]- ∞, h]	croissante dans [- 5, + ∞ [
Zéros de la fonction	C'est la valeur z de x, tels que f(x) = 0. Si elle existe.	Le zéro est : z = - 1
Ordonnée à l'origine	Valeur de f(x = 0)	f(0) = 5√6 - 12 = 1.42
Signe de la fonction f	• f(x) est positive ou nulle dans l'intervalle solution de l'équation f(x) ≥ 0. • f(x) est négative dans l'intervalle solution de l'équation f(x) < 0.	contrainte : x ≥ - 5. solution: x + 5 = 4 , x = - 1 f(x) est positive ou nulle dans [- 1, + ∞[, f(x) est négative dans [- 5, - 1[
Extremums	• Si a > 0, la valeur minimale est k. • Si a < 0, la valeur maximale est k.	La fonction a un minimum de - 12.
Graphique de la fonction

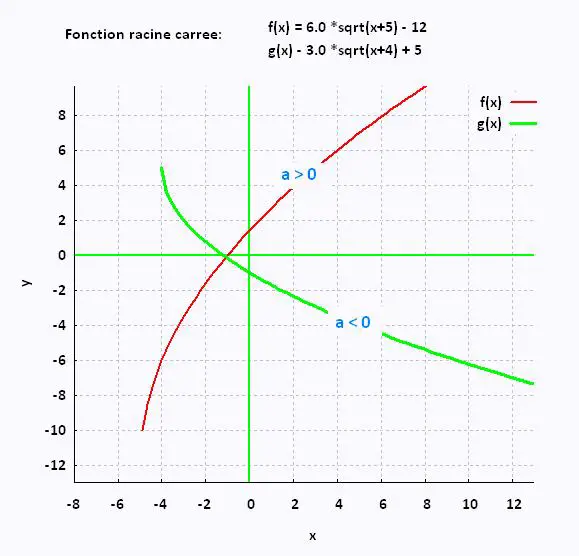
Pour imprimer un modèle de table des propriétés d'une fonction racine carrée : table des propriétés